A recent Design Idea (Ref. 1) presents a circuit to measure an airflow rate up to 2000 fpm using two transistors in a Darlington configuration. One transistor works as a self-heated thermal sensor and the other one compensates for ambient temperature variations. The circuit is smart and simple; however, the output voltage depends on the input flow rate in a very nonlinear fashion. The paper presents two hardware options to linearize the sensor response, which reduce nonlinearity to about 10-12% of the maximum flow rate.
Modern microcontrollers offer significant calculation power, sometimes at a very low price, so it is worth trying to find a calculation solution to the nonlinearity problem.
Before we start, let’s recall the principle of linearization: the circuit or the calculation formula that will process the output signal of the sensor circuit must generate the inverse function of the sensor response. For example, if the sensor response is a log function, the response of the linearizing section must be exponential.
The work started with getting 46 discrete points of the sensor response (see Figure 4 in the reference paper). The discretion step is small at the beginning where the curve rises fast and gets bigger as the curve becomes more and more flat. Attempts to fit the flow rate versus voltage response with a piecewise approximation or cubic splines can reduce linearity error to 1-2% at the cost of bulky formulas. It would be much better if the whole curve is covered by a single smooth function.
Several functions of different complexity were tested. The best results were achieved with a composite function of the form:
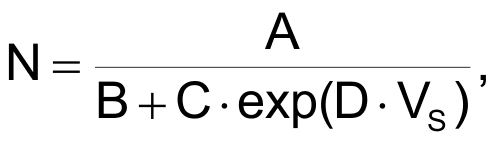
where N is the number to be generated by the microcontroller and VS is the output voltage of the sensor circuit. The presence of four coefficients, A to D, provides a lot of flexibility to fit the desired set of points.
The Solver tool of MS Excel found the proper values of the unknown coefficients:
A = 10525.4,
B = –4.49563,
C = 9103.05 and
D = –1.36567.
 |
|
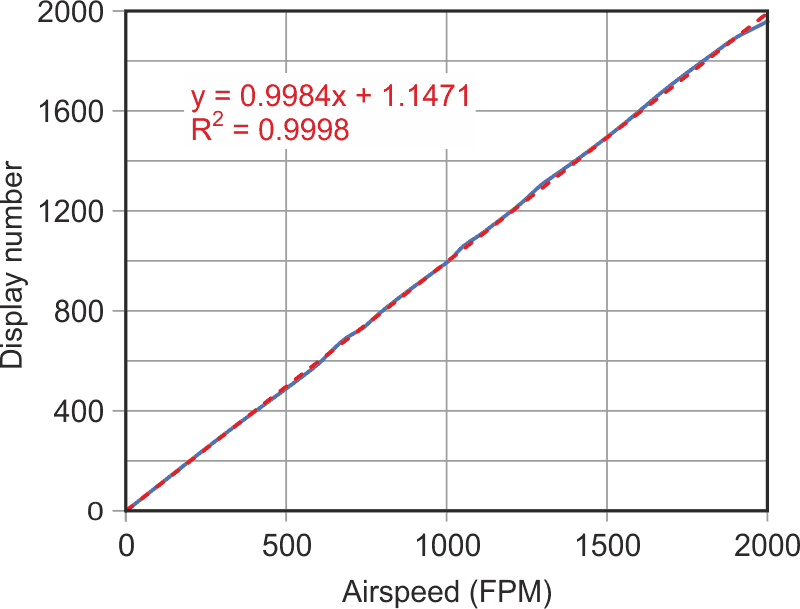
| Figure 1. | The calculation approach provides a highly linear, 1:1 relation between the displayed number and the airflow rate. |
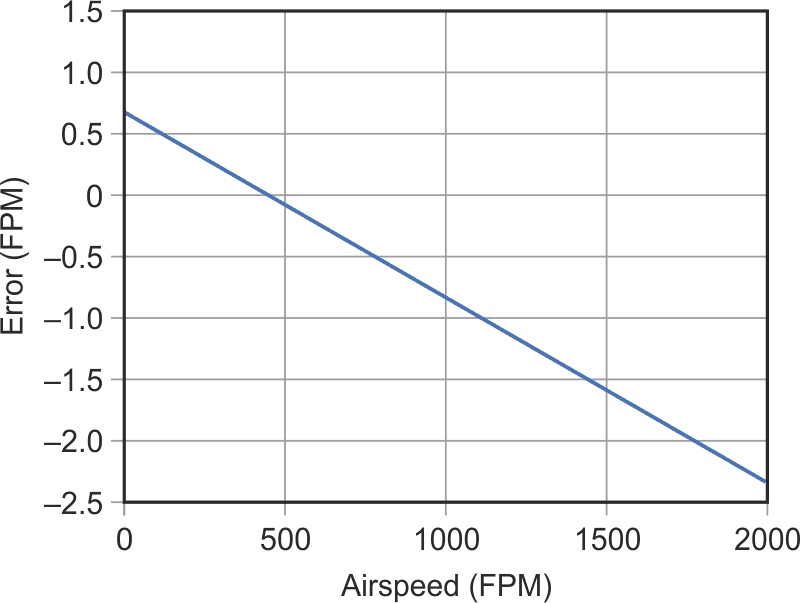
As Figure 1 shows, passing the sensor voltage through this function provides a highly linear relation between the number N to be displayed and the flow rate. Figure 2 presents the deviation between the discrete points of the response and the best fit linear equation. The error is within the ±2.5 fpm range, which is 0.125% of the maximum flow rate. This is 80 times better than the hardware solutions in the reference paper. An important feature is that the error will affect only the last digit in the displayed number.
 |
|
| Figure 2. | Close insight reveals a very small nonlinearity of the overall response. |
In real applications, the error may not be that small due to errors in the A-to-D conversion, limited size of numbers and rounding errors during the calculations; however, it will be still much better than the hardware solutions.
If the proposed function looks too complicated to you, feel free to try any other function you may wish. Uncheck the “Make Unconstrained Variables Non-negative” box, so the unknown coefficients can get negative values.
Reference
- Woodward, Stephen. "Nonlinearities of Darlington airflow sensor and VFC compensate each other."