If you need a very pure sine wave in the audio range, the circuit in Figure 1 can help. It is a simple deal: A sine wave with a THD of 1% coming from a function generator that goes through a trackable low-pass filter, which attenuates the distortion-causing harmonics by a factor of 7900 (–78 dB) or more. The result is a sine wave with less than 0.0002% (2 ppm) distortion.
 |
|
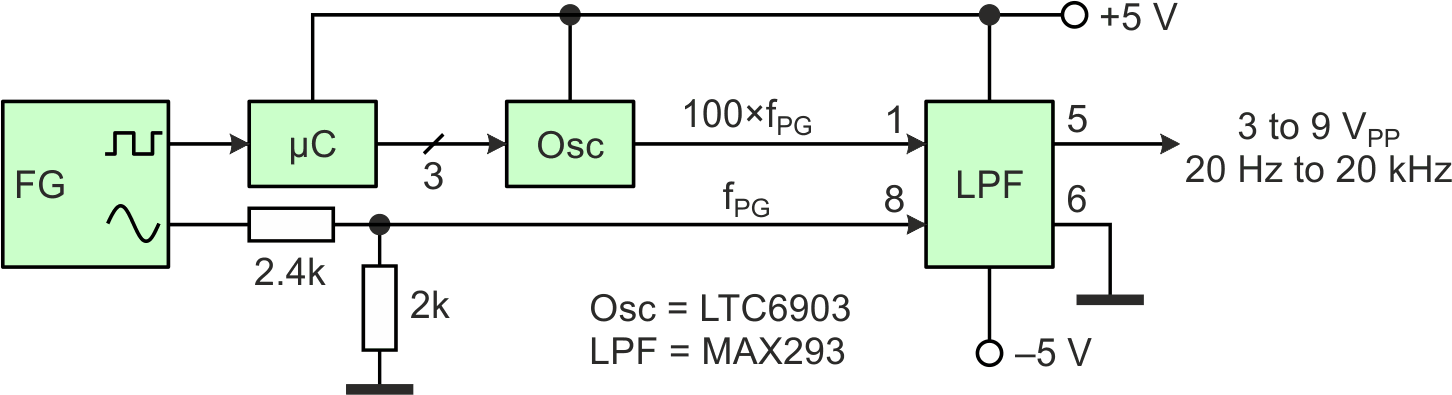
| Figure 1. | A frequency multiplier and a tracking low-pass filter reduce the THD of the sine signal coming from a function generator by 78 dB or more.. |
This implementation’s advantage comes from the fact that function generators provide two signals, a sine wave and a square wave, with the same frequency. The sine wave goes to the low-pass filter. A voltage divider reduces amplitude so that it does not exceed the input range of the filter. The switched-capacitor filter needs a clock signal with frequency that is 100 times larger than the frequency of the signal being filtered. The microcontroller–oscillator pair generates the clock signal. The microcontroller (µC) measures the frequency of the signal coming from the function generator, multiplies it by a factor of 100, creates a 16-bit control word, and sends it to the oscillator through an SPI interface. The oscillator generates a square-wave signal for the filter. The corner frequency of the filter equals the fundamental frequency of the input voltage.
 |
|
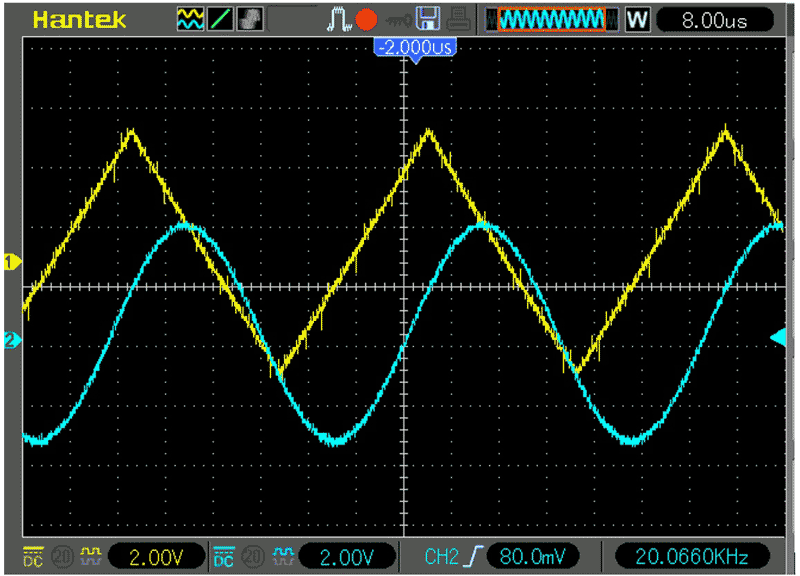
| Figure 2. | The time domain signals from the function generator and at the output of the filter. |
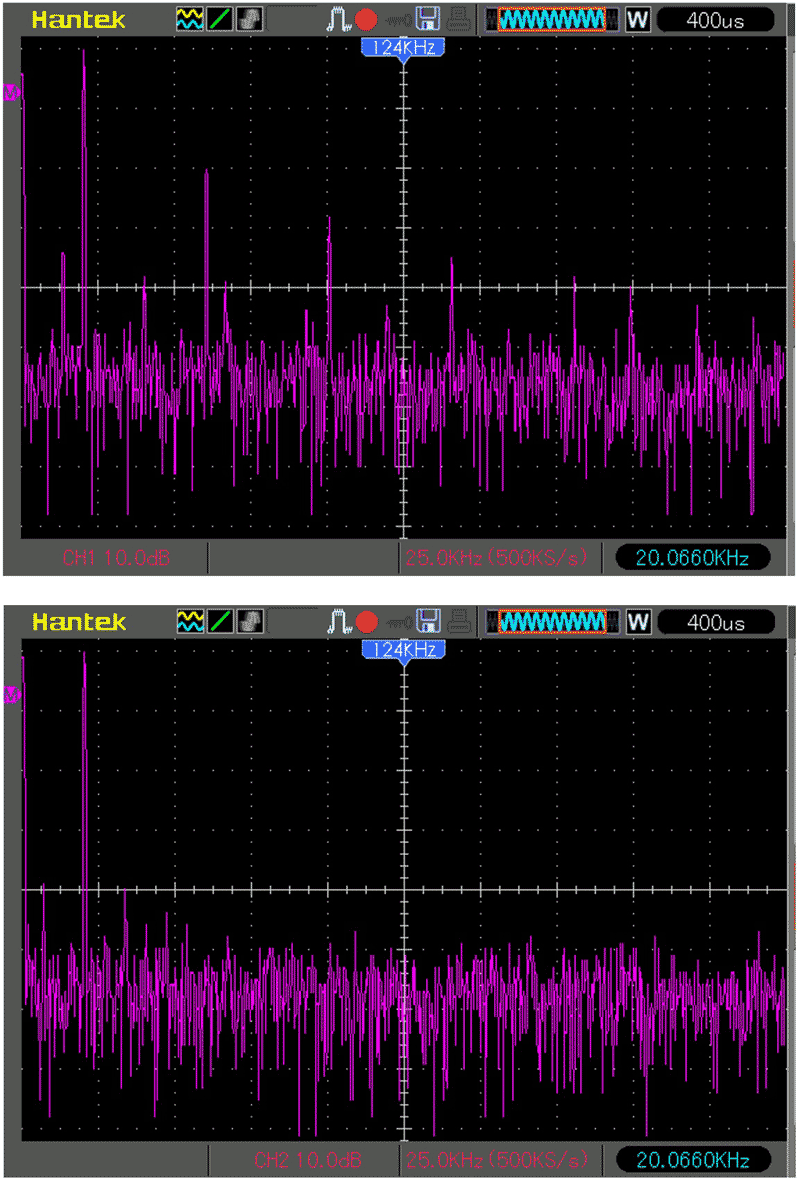
Figure 2 and Figure 3 demonstrate the circuit operation with a 20-kHz triangular signal. Figure 2 shows the time domain signals from the function generator and at the output of the filter. Figure 3’s images are the spectrums of these signals. The filter passes the fundamental frequency and reduces the distortion-making harmonics down to the noise floor. The difference between the fundamental and the floor is about 50 dB, which is normal for the 8-bit ADC of the oscilloscope. More sophisticated (and more expensive) equipment is required to catch the difference of about 80 dB expected for the sine wave. Curious readers can get a sense of this business in references [1-4].
 |
|
| Figure 3. | The spectrum of the 20-kHz triangular signal: the fundamental harmonic is 50 dB above the noise floor. More sophisticated equipment is required for the sine wave. |
It is worth mentioning that the same approach has been used to filter a square wave signal or a digitally generated sine wave with a very small number of stairs, see references [5-7]. Despite the large attenuation of the filter, the output signal is not a pure sine wave due to the high level of harmonics in the input signal: 43% for the square wave and 11-12% for a “sine” wave made of five stairs. The proposed circuit uses an input signal with 1% distortion (analog function generators) or 0.1% distortion (DDS-based function generators); hence the output signal will be at least 10 or 100 times cleaner than with the previous circuits.
If you decide to make the circuit, measure the period, not the frequency of the signal coming from the signal generator. The longest measurement time will be 50 ms instead of seconds.
Also, make sure you fill the period interval with at least 1000 clock pulses; the goal is to get 0.1% accuracy. This means clock rate of 20 MHz or more for the shortest period of 50 µs. Lower clock rates should be used for longer periods to avoid getting too large numbers for the captured clock pulses.
Finally, keep the sine signal amplitude from 3 to 9 VPP. This is the range where the filter provides minimum distortion and noise.
References
- Williams J., G. Hoover. Test 18-bit ADCs with an ultrapure sine-wave oscillator. EDN, Aug. 11, 2011, 19-23.
- Janasek V. An ultra low-distortion oscillator with THD below -140 dB.
- ARTA software
- TSP #234 – QuantAsylum QA403 24-bit, 0.0001% THD Audio Analyzer Review, Teardown & Experiments
- Horowitz P., W. Hill. The art of electronics. 3rd, 2015, pg. 436.
- Saab A. Locked-sync sine generator covers three decades with low distortion. EDN, Sep 18, 2008.
- Elliot R. Sinewave oscillators, Section 8 – Digital generation.