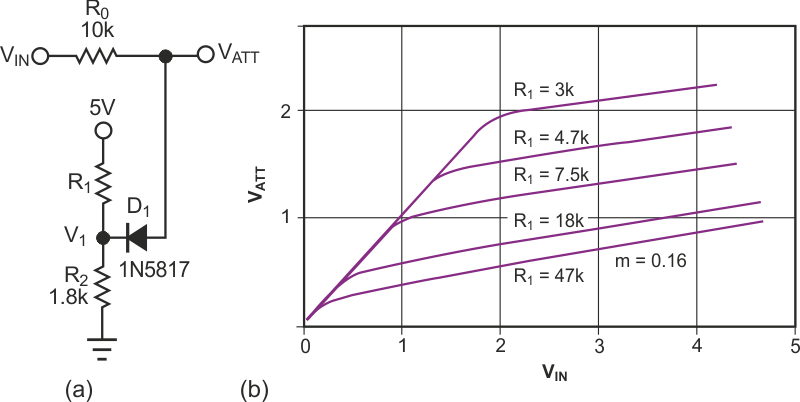
In analog design, you might need to create an amplifier with nonlinear dynamic characteristics – for example, logarithmic, exponential, or square-law. Usually, such amplifiers are complicated. However, the project often does not require mathematical precision. For example, you might just need to increase the dynamic range of an amplifier, or to eliminate saturation for an extended input-voltage range. The Design Idea is based on the nonlinear voltage attenuator with the attenuation ratio m = VATT/VIN, controlled by the input voltage (Figure 1a). When VIN is small enough to hold off D1, m = 1. When the input voltage increases and attains a certain threshold voltage, VTH, the diode conducts, and the attenuation ratio decreases.
 |
||
| Figure 1. | Manipulating the resistor values in an attenuator (a) changes the threshold for nonlinearity (b). |
|
The new value of m depends on the values of R0 and R2. R1 and R2 determine the threshold level, VTH. Hence, you can estimate the resistors R1 and R2 for a given R0, VTH, and m as:
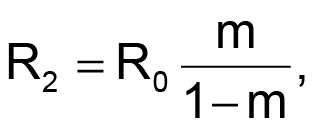
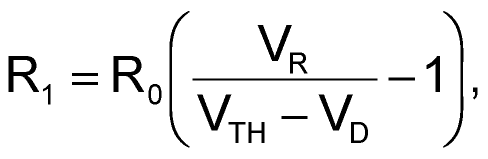
where VD is the drop across diode D1, and VR is the dc voltage applied to R1 and R2.
 |
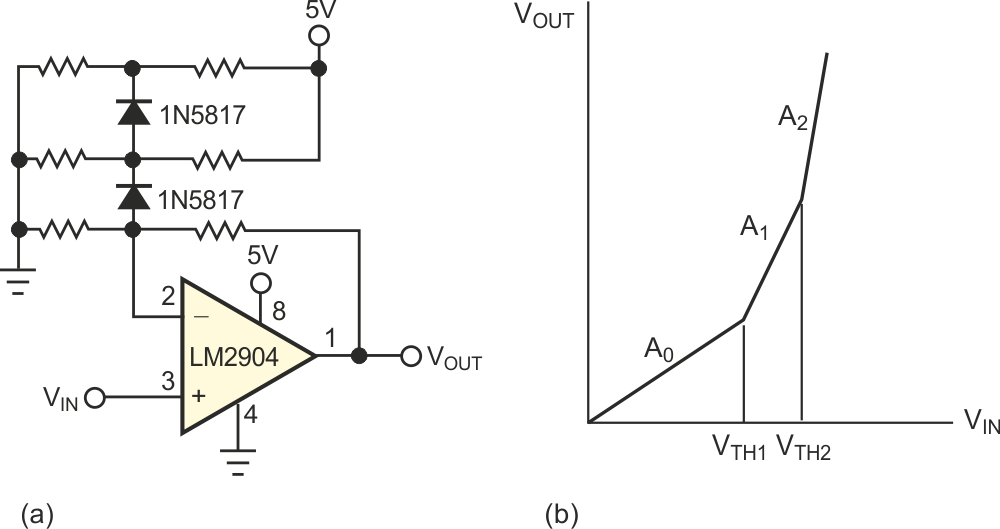
||
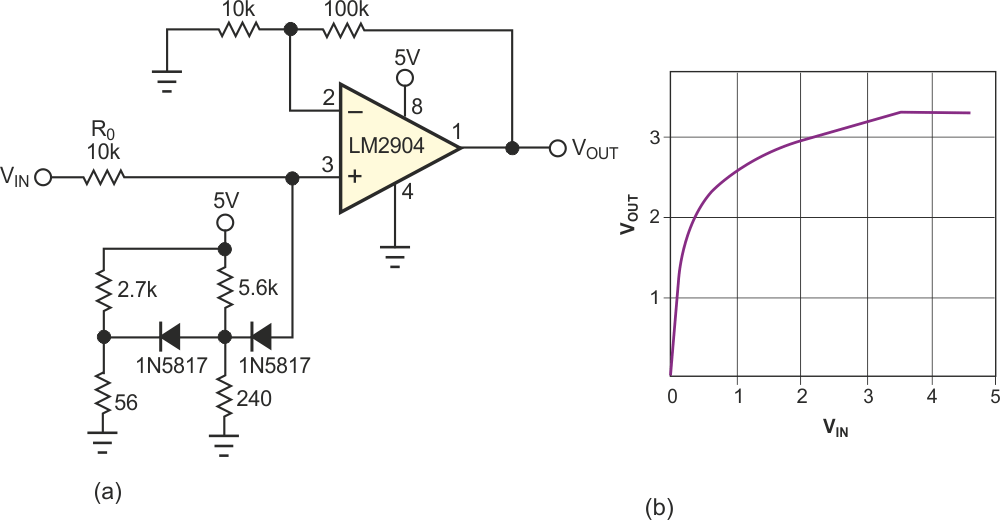
| Figure 2. | A multistage nonlinear attenuator (a) can increase the dynamic range of an amplifier (b). | |
Note that you can create any characteristic by choosing the proper ratio, m, and the threshold voltage for each fragment of the resulting characteristic. Also, the linear approximation is good for calculation purposes, but the real ratio changes smoothly near the threshold voltage. Finally, use Schottky diodes to increase the voltage range of regulation. Figure 1b shows the dynamic response of the attenuator for the constant ratio m = 0.16 but for different threshold voltages. The measured voltage is V1 = VTH – VD. To increase the dynamic range of an amplifier, you should put the nonlinear attenuator at the input of the amplifier. To widen the range, you can use a two-stage attenuator. Figure 2 (right) shows such an amplifier and its recorded characteristic. The applications of the nonlinear attenuator are not limited to increasing dynamic range. You can obtain a square-law response, for example, by putting the attenuator in a feedback circuit (Figure 3).
 |
||
| Figure 3. | A nonlinear attenuator in the feedback loop (a) results in a square-law characteristic (b). | |