Mikhail Shustov, Tomsk
The description and diagram of the electronic analogue of the parallel-oscillatory circuit with continuously tunable frequency are given.
A detailed review of the main types of RC-electronic, resonant, cut-off, blocking, and the other filters is given in the monograph [1].
Gyrator filters, in which the set of RC-elements and an operational amplifier is converted into an equivalent LR-circuit, have become the most widespread as RC-resonance filters, effectively working in the low-frequency region [1, 2]. However, the range of circuit solutions in terms of creating a new generation of filters is nowhere near exhausted.
In works [3, 4] an original approach to use the invariance properties of circuit functions in the synthesis of active circuits for creating amplitude-frequency distortion correctors as well as generators was proposed.
Based on the ideas presented in [3, 4], it is easy to synthesize new types of filters [5, 6], one of the variants is presented below in Figure 1.
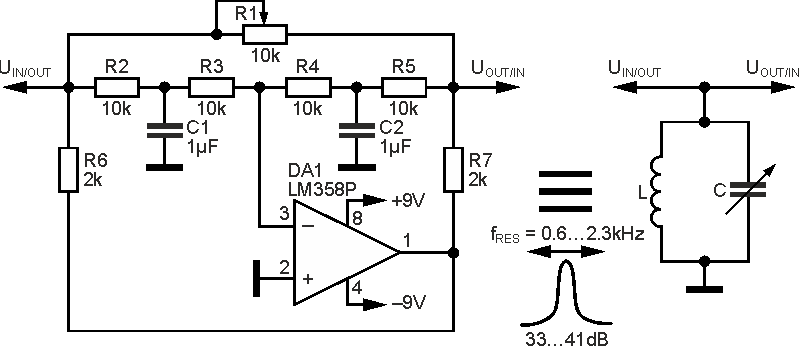 |
||
| Figure 1. | The analogue of the parallel low-frequency electronic tunable LC-oscillatory circuit. | |
The resonant filter is an analogue of the parallel low-frequency LC-oscillatory circuit, made according to a symmetrical scheme using operational amplifier LM358P as an active element. With the elements indicated in the diagram, the filter can be adjusted with potentiometer R1 in the range from 0.6 to 2.3 kHz. It is recommended to install a limiting resistor of 100 Ohm in series with this potentiometer.
The equivalent Filter Quality goes down from 60 to 18, when the frequency is lowered. The transfer coefficient at a maximum transmission peak, depending on the frequency under the same conditions, falls from 41 to 33 dB.
The input and/or output shunting of the electronic analogue of the oscillating circuit with an active resistance of less than 300 kOhm in full analogy with the real LC-oscillating circuit reduces its equivalent q-factor.