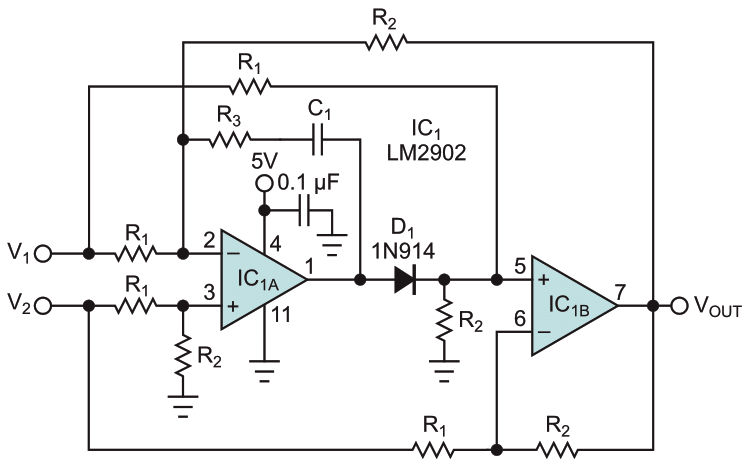
A traditional implementation of an absolute-difference function comprises a difference circuit followed by an absolute-value circuit; the entire circuit requires at least three op amps. The design problem is complicated in single-supply-only systems, which usually require an artificial ground, typically one-half of the supply. The circuit in Figure 1 takes the absolute value of the difference of two voltages using only two single-supply, ground-referenced op amps. The circuit is designed for dc or low-speed operation.
 |
|
| Figure 1. | Using single-supply, ground-referenced op amps, this circuit accomplishes an absolute-difference function. |
For the case where V1 > V2, IC1A is disabled because diode D1 is off. IC1B and its associated resistors form a classic difference circuit where
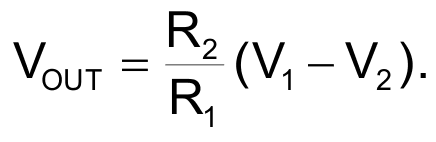
For the case where V2 > V1, diode D1 conducts, producing the composite amplifier system made up of both IC1A and IC1B, where
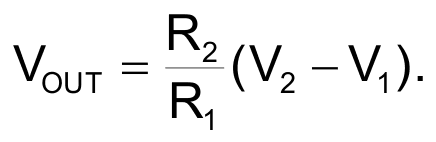
Using these two equations, the overall function of the circuit for V1 and V2 greater than zero is as follows:
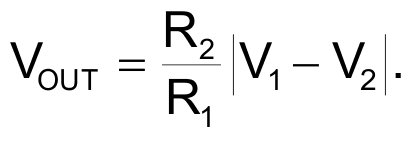
The circuit was built and tested with R1 = 0 Ω and R2 = 20 kΩ. For V2 > V1, the composite amplifier system has poor phase margin and is unstable. Thus, the circuit compensates the loop with the dominant pole formed by R3 and C1. At a gain of 22 and a desired response time of about 300 μsec (the 10 to 90% rise time when V2 becomes 0.1 V greater than V1), values of R3 = 56 kΩ and C1 = 850 pF produced the best empirical results. R3 and C1 will vary, depending on the required speed of the response and the closed-loop gain.
Also, when V2 > V1, the output of IC1A becomes a function of the factor 2V2 – V1. Thus, IC1A may saturate for large values of V2. The factor’s upper limit is as follows, where VSAT is the saturation voltage for IC1A:
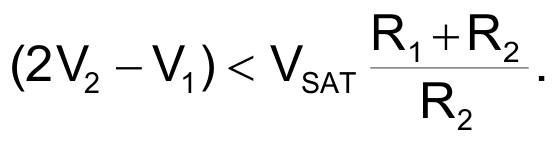
For the LM2902 operating from 5 V, VSAT is approximately 3.5 V. This last equation also implicitly sets a common-mode voltage (VCM) limitation. You can see this limitation by setting V1 = V2 = VCM and allowing the factor (2V2 – V1) to reduce to VCM.