Matt Kornblum
EDN
The circuit in Figure 1 converts a ±10 V analog voltage representing an angle between θMIN and θMAX and emits a voltage equal to 10·cosθ. This circuit can have an accuracy of better than 1% over ±120° or better than 0.2% over ±90°. These figures represent an order-of-magnitude improvement over a Taylor-series estimate for the same range and for the same number of multiplications. The Taylor-series definition for a cosine (with θ in radians) is:
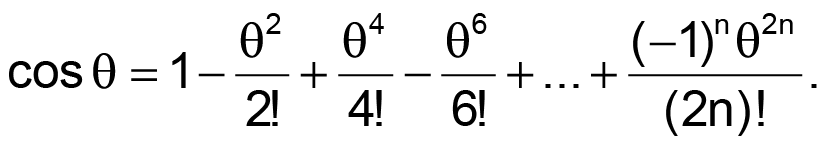
The series works well for high values of n or small angles. Generally, for n = 2, significant errors start to accumulate for angles exceeding ±45°. When you use a Taylor-series expansion for better accuracies at larger angles, the number n becomes larger and demands more resources from the design. The Taylor series for n = 2 has the form of
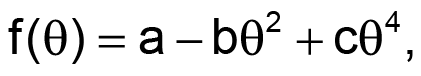
where a = 1, b = 0.5, and c = 0.041667 (for angles in radians). By using a least-squares curve fit to optimize this function at n = 2, you can find coefficients that allow you to obtain significantly better accuracies over the desired input range without raising the value of n to more than 2. The circuit in Figure 1 embodies this least-squares approach.
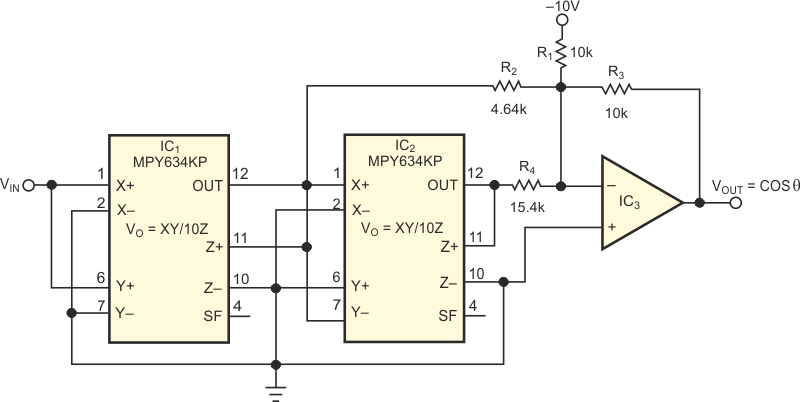 |
||
| Figure 1. | By manipulating Taylor-series coefficients, you can obtain better accuracy when generating cosines. | |
Choosing the resistor values for the circuit is relatively simple. Set R1 and R2 equal to each other (for 10 V maximum input and a ≈ 1), and determine values for R2 and R4 by applying the following equations:
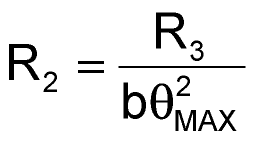
and
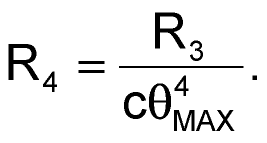
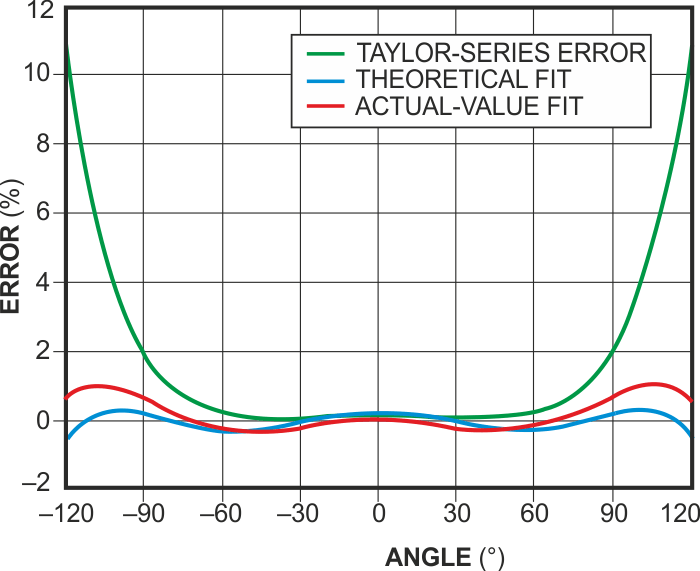
IC1 generates the square of VIN and negates it. This output sums through R2 into IC3. IC2 generates the fourth power of VIN and sums it into IC3 through R4. A –10 V reference across R1 creates the "a"-coefficient constant current into IC3. The output of IC3 is the sum of the three terms. Because IC1 is an inverting amplifier, the circuit configures the multipliers such that the output of IC1 is positive and the output of IC2 is negative. Choosing the proper 0.1% resistors can improve circuit accuracy to better than 1% for –120° to +120°. You should use a low-offset op amp for best results. Figure 2 shows the Taylor-series error, the theoretical fit, and the actual fit. For a fit in a 90° range, the values change slightly, and the errors across the range become significantly smaller. The constant "a" becomes 0.9996, b=0.4962, and c=0.0371. Then, R1=R3=10 kΩ, R2=8.16 kΩ, and R4=44.2 kΩ.
 |
||
| Figure 2. | For angles greater than 90, the revised coefficients in Figure 1 yield significant accuracy improvements in calculating cosines. |
|
You can use the same approach to efficiently calculate cosine and sine values in a DSP system more rapidly than using a look-up table.