Analog switch converts 555 timer into pulse-width modulator

This Design Idea describes a new approach to producing a variable-duty-cycle waveform from a 555-based free-running oscillator. The circuit's wide modulation range, highly linear control over a wide range of duty-cycle values, and excellent linearity make it ideal for PWM (pulse-width-modulation)-based control applications. Figure 1 shows the basic circuit, which works as follows: When IC₁'s output goes high, switch S₁ closes, and IC₁'s internal discharge, switch S₂, opens. Capacitor C₁ charges through R₁ and R₂. When IC₁'s output goes low, S₁ opens, and S₂ closes, discharging C₁ through R₂ and R₃.

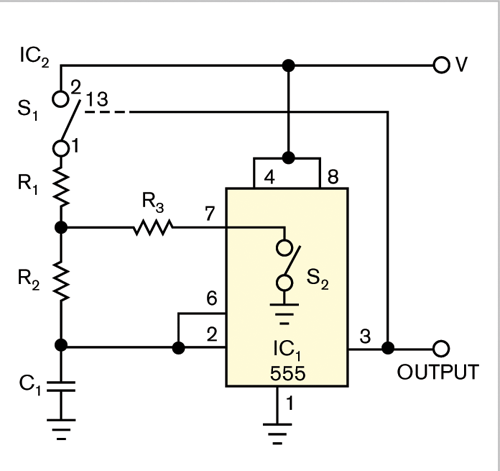
Figure 1 An external analog switch and a 555 timer
provide a free-running oscillator with a fixed duty cycle.

The generic configuration works well for producing a fixed-value duty cycle. To obtain a continuously variable duty cycle, Figure 2 shows how to connect potentiometer R₄ to the common junction of R₁, R₂, and R₃. The output waveform's duty cycle, D_TC, follows the equation:

D_TC=(R₁+R₂+R_VAR)/(R₁+2R₂+R₃+R_POT)

where R_POT is the potentiometer's end-to-end resistance, and R_VAR is the fraction of R_POT between the rotor and R₁. As the equation shows, D_TC depends linearly on R_VAR. Switch S₁ comprises one section of a 4066 CMOS quad bilateral SPST switch, IC₂.

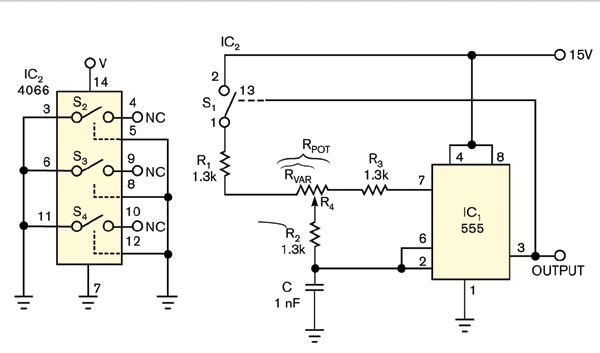
Figure 2 Add a potentiometer, R₄, to produce an output pulse that has a manually variable duty cycle.

You can use the circuit in Figure 3 to evaluate duty-cycle linearity. A rotary switch and a tapped series string of 16-kΩ resistors provide a 10-kHz signal with nine discrete, equally spaced duty-cycle values ranging from 2 to 98%. For accurate results, use a 5½-digit multimeter to match the values of resistors R₄ through R₁₁ and a Tektronix 3012 oscilloscope or equivalent to gather D_TC data.

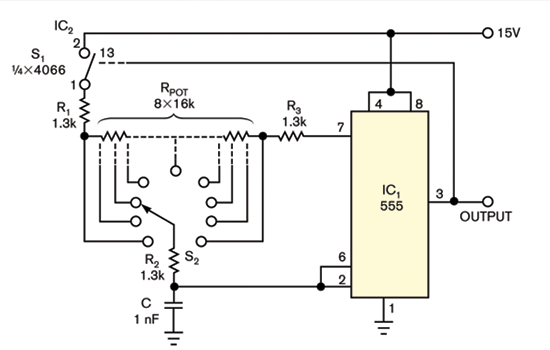
Figure 3 To obtain fixed-duty-cycle values for linearity evaluation,
you can replace the potentiometer with a rotary switch
and a series-connected string of precision resistors.

Microsoft's Excel-spreadsheet software includes a linearity analysis that returns the following trend line for the duty-cycle measurements:

D_TC=0.7565×R_VAR+2.1548; R₂=1.

The value of 1 for R₂ as Excel calculates shows that the transfer function is perfectly linear. Switch S₁'s on-resistance and particularly its leakage current slightly affect the D_TC-versus-R_VAR equation's slope and intercept, but the equation remains strictly linear. Using only one of IC₂'s four switches eliminates leakage effects and crosstalk that would occur if other circuits used the remaining switches. In addition, using moderately low values for the resistor network further reduces leakage-current effects on circuit performance.