Glen Brisebois
EDN
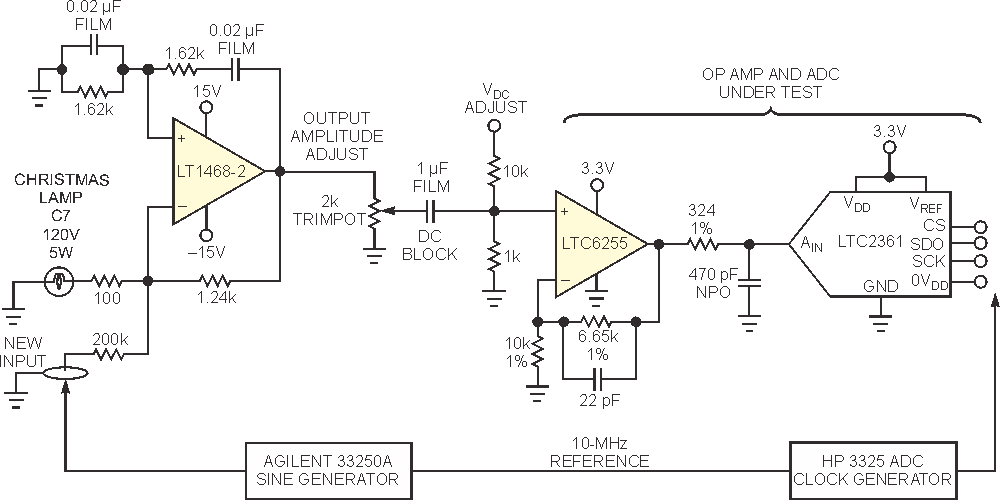
I recently had the opportunity to investigate a new micropower 6-MHz LTC6255 op amp driving a 12-bit, 250k sample/sec LTC2361 ADC. I wanted to acquire the FFT of a pure sinusoid of about 5 kHz. The problem is that getting the FFT of a pure sinusoid requires, well, a pure sinusoid. Most programmable signal generators, however, have fairly poor noise and distortion performance, not to mention digital “hash” floors, compared with dedicated op amps and good ADCs. You can’t measure 90-dB distortion and noise using sources that are “60 dB-ish.” So rather than try to find and keep an almost-ideal programmable signal generator, I decided to build up a low-distortion Meacham-bulb-stabilized Wien-bridge oscillator using an ultralow-distortion LT1468-2 op amp (Figure 1).
 |
||
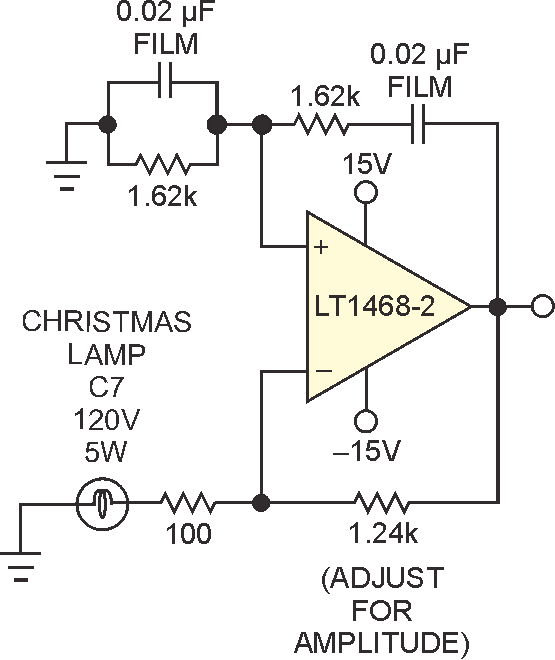
| Figure 1. | This Meacham-light-bulb-stabilized, low-distortion, low-noise 5-kHz Wien-bridge sinusoidal oscillator’s RC feedback network attenuates by a factor of 3 at its midband. The bulb’s self-heating forces a gain of 3 in the op amp. |
|
The lightbulb amplitude-stabilization technique relies on the positive temperature coefficient of the bulb impedance stabilizing the gain of the op amp to match the attenuation factor of 3 in the Wien bridge at its center frequency. As the output amplitude increases, the bulb filament heats up, increasing the impedance and reducing the gain and, therefore, the amplitude. I did not have immediate access to the usually called-for 327 lamp, so I decided to try a fairly low-power, high-voltage bulb, like the C7 Christmas bulb shown. At room temperature, it measured 316 Ω; fresh out of the freezer (about –15 °C), it measured 270 Ω. Based on the 5 W, 120 V spec, it should be about 2.8 kΩ at white hot. That seemed like plenty of impedance range to stabilize a gain of 3, so I decided to linearize it a bit with a series 100 Ω resistor.
For a gain of 3, the bulb plus 100 Ω must be half of the 1.24 kΩ feedback (or equal to 612 Ω), so the bulb must settle at 512 Ω. Roughly calculating a resistance temperature coefficient of
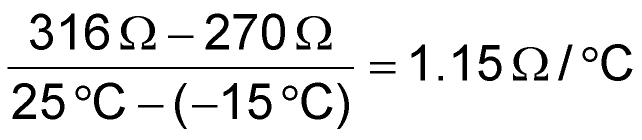
means that the bulb filament will be about 195 °C.
 |
||
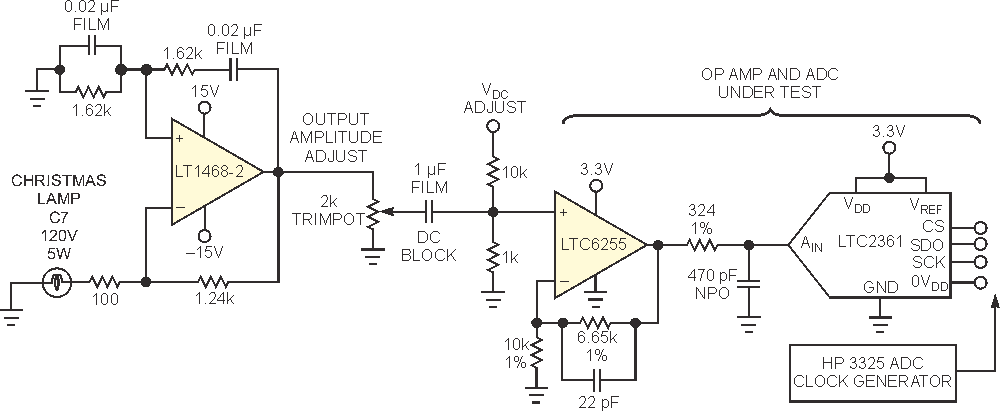
| Figure 2. | The Wien-bridge oscillator drives the op amp and ADC pair under test. The resulting FFT is clean after windowing, but not exceptional, as Figure 3 shows. |
|
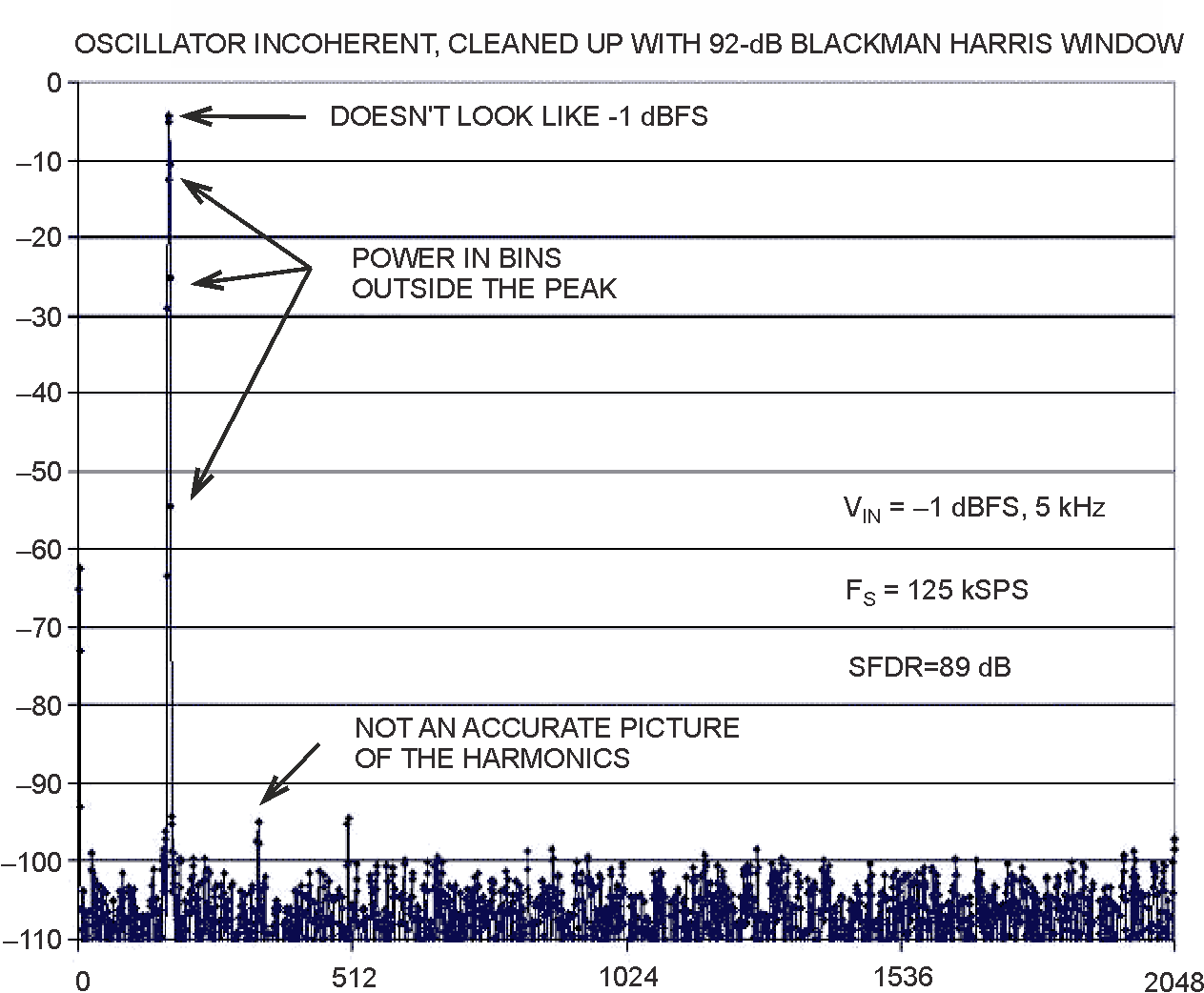
The oscillator powered up fine, giving a nice sinusoidal 5.15-kHz output at several volts, and independent measurements showed the second- and third-harmonic distortion products to be lower than –120 dBc. I applied the oscillator to the LTC6255 op-amp input after blocking and adjusting the dc level and ac amplitude, using the caps and pots as shown in Figure 2. The ac amplitude was adjusted for –1 dBFS, and the dc level was adjusted to center the signal within the ADC range. But, of course, this oscillator was purely analog and had no “10-MHz reference input” on the back to allow it to be synchronized with the ADC clock. The result is substantial spectral leakage in the FFT, so that it looks more like a circus tent than a single spike. Applying a 92-dB Blackman-Harris window to the data to reduce FFT leakage produced a fine-looking FFT (Figure 3).
 |
||
| Figure 3. | This 4096-point FFT was achieved using an unlocked oscillator with a 92-dB Blackman-Harris window. Note that the peak does not look like –1 dBFS and that there is power in the bins around the peak. |
|
Although this FFT is accurate in some ways, a closer inspection reveals some problems. For example, the input signal is –1 dBFS, but it certainly looks graphically lower than –1 dB down. The reason is that even an excellent windowing function leaves some of the fundamental power in the frequency bins adjacent to the main spike. The software includes these bins in its power calculations, and rightly so, but the fact is that the spike looks too low to make a good photograph.
The same can be said about the height of the harmonics; although they are calculated correctly and are accurate relative to the fundamental, they also look too low in absolute terms. So windowing is no substitute for a coherent phase-locked system.
When those objections were raised, I despaired that I was going to have to return to the drawing board and maybe stay there, or find a locked oscillator with low distortion and noise or with awesome postfiltering. How could I ever make such a fundamentally analog oscillator coherent to an FFT bin in such an overwhelmingly digital environment? At 5 kHz, a passive filter with notches would be large and fussy. I thought of detuning the Wien-bridge oscillator by reducing the gain, thereby converting it into a filter.
But then it occurred to me that a gentle, analog sinusoidal nudge from a distorting but well-locked external oscillator might be enough to tweak the Wien-bridge frequency to where it needed to be. I decided to try injecting a sinusoid into the input of the Wien-bridge op-amp circuit, and opted to use a high series impedance to avoid simultaneously injecting noise and distortion. I came up with 200 kΩ – about 1000× the impedances already there – and put it in as shown on the left side of Figure 4 (the “new input”). I set up the Agilent 33250A for a 5-kHz sine wave and applied it to the new input. Looking at both the 33250A and the Wien-bridge outputs with an oscilloscope, I slowly dialed up the 33250A frequency and was thrilled to finally see the sinusoids come “close” and then snap into lock.
 |
||
| Figure 4. | With the generators phase locked through the 10-MHz reference, the low-noise and -distortion Wien-bridge oscillator is gently nudged into coherence through the high-impedance, 200k resistor. |
|
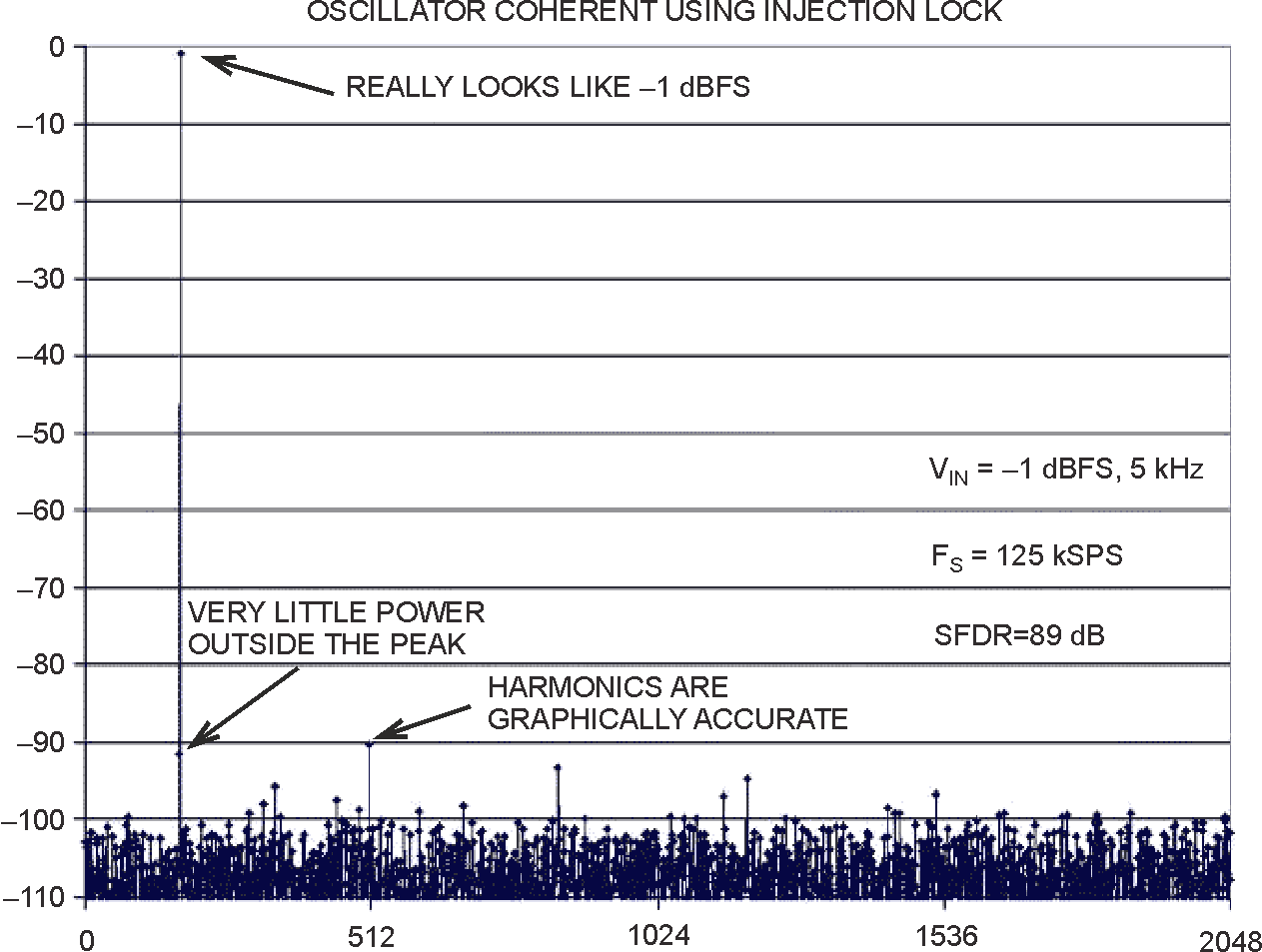
I connected the 10-MHz back-panel references and changed the 33250A frequency to 5.157 kHz, the nearest coherent bin in the FFT. The sinusoids remained in lock, and the programmable 33250A generator successfully pulled the Wien-bridge oscillator slightly away from its natural frequency and into the desired frequency. The result was a nearly ideal FFT; all of the pertinent fundamental and distortion powers were situated in unique bins and were accurately represented (Figure 5).
 |
||
| Figure 5. | A more accurate FFT is obtained using the same Wien-bridge oscillator but with the frequency injection locked to a coherent 5.157 kHz using an HP33250A driving the 200k resistor at the “new input.” Note that the peak is now visibly a believable –1 dBFS and that there is almost no power in the bins adjacent to the peak. |
|
Programmable sinusoidal generators often have excellent phase-noise characteristics and 10-MHz locking capabilities, but they also have high-output wideband noise floors and distortion. An FFT is sensitive to all of these forms of source corruption and also has a finite number of output bin frequencies. To test high-performance analog and mixed-signal systems, the right combination of classical Wien-bridge oscillators with programmable generators can provide a nearly perfect source with synchronous sampling, generating accurate FFTs.
