Fan noise is becoming a significant issue as electronic equipment increasingly enters the office and the home. Noise is proportional to fan speed, and the airflow – hence, fan speed – necessary for cooling is less at low ambient temperatures. Because ambient temperature is lower than the upper design point most of the time, a fan can run slower, making it easier on the ears. Fan-control circuits range from simple switches that boost the speed from low to high, to digital, proportional speed-control designs. High/low-speed switches are inexpensive, but the sound of sudden speed changes can be annoying. Digitally controlled fans perform well, but the circuitry is costly, and the system must include a serial bus.
 |
||
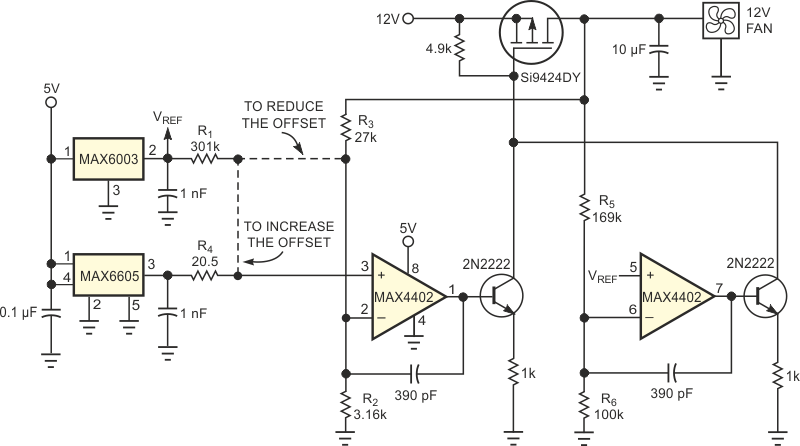
| Figure 1. | This circuit delivers a continuous and linear fan-control voltage that is proportional to temperature. | |
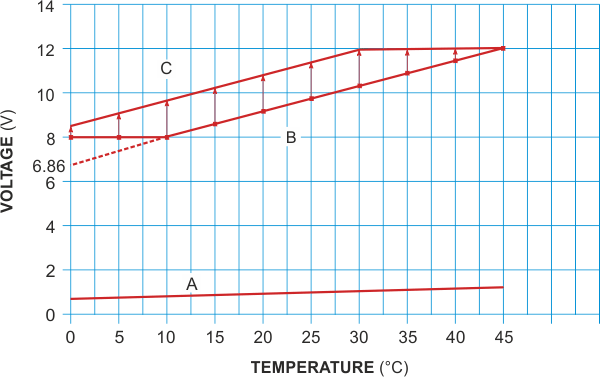
As an alternative, consider a low-cost, self-contained analog circuit for fan-speed control (Figure 1). You can easily adjust the circuit for any desired linear relationship between the fan voltage and temperature (Figure 2, curves B and C). We plotted measured data points against the desired voltage in Figure 2.
 |
||
| Figure 2. | These curves illustrate voltage output versus temperature for the circuit in Figure 1. | |
Curve A in Figure 2 represents the output of a MAX6605 analog temperature sensor versus temperature in degrees Celsius:
VSENSOR = 0.0119 V/°C + 0.744 V.
Curve B relates the fan voltage to temperature and combines a minimum “floor” voltage of 8 V with a sloping line:
VFAN = 0.114 V/°C × T + 6.86 V,
where T is the system temperature.
The floor voltage ensures fan rotation at low temperatures. Above 10 °C, the voltage increases with a slope of 0.114 V/°C until it reaches full value at 45 °C. Simply amplifying the MAX6605's output does not provide the 8 V floor voltage. Moreover, the gain
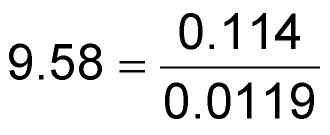
needed to obtain the fan-voltage slope is not the same gain
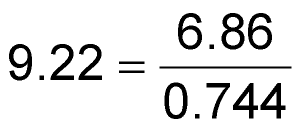
needed to obtain the y-intercept point.
To transform Curve A into Curve B, you must subtract a voltage offset from the temperature sensor's output and then multiply the result by a constant. The circuit in Figure 1 performs this operation. You connect the dotted line labeled “To reduce the offset.” One op amp creates the sloped line, and the second op amp creates the floor voltage. The op amps' outputs connect to transistors in such a way that the op amp demanding a higher output voltage dominates. The following equations allow you to determine resistor values:
For the condition in which R2 << R1, R1 = any reasonable value;
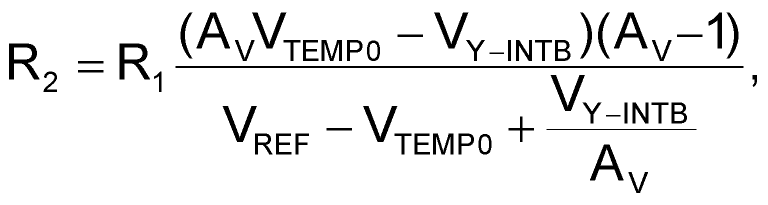
and
R3 =R2(AV – 1),
where AV = 0.114/0.0119 = 9.58 = the ratio of the desired slope in volts per degrees Celsius to that of the sensor; VTEMP0 = 0.744 V = the temperature-sensor voltage at 0 °C; VY-INTB = 6.86 V = the y-intercept indicated by the desired (extrapolated) temperature curve; and VREF = 3 V = the reference voltage.
Thus, choosing R1 = 301 kΩ lets you calculate R2 = 3.158 kΩ and R3 = 27.09 kΩ. The closest 1% values are 3.16 and 27 kΩ, respectively. The following equation lets you calculate the floor voltage:

where R6 equals any reasonable value, VFLOOR = 8 V, the desired minimum output voltage.
Thus, choosing R6 = 100 kΩ lets you calculate R5 = 169 kΩ. In some cases, the required offset gain is greater than the required slope gain, so you must increase the temperature sensor's natural offset. For a desired temperature, Curve C, expressed as
VFAN = 0.114 V/°C × T + 8.5 V,
the gain (slope) of AV = 9.58 is the same as for Curve B, but the required offset gain is (8.5/0.744) = 11.42 is greater. You therefore use the “To increase the offset” version of the circuit in Figure 1. The following equation applies in such cases:
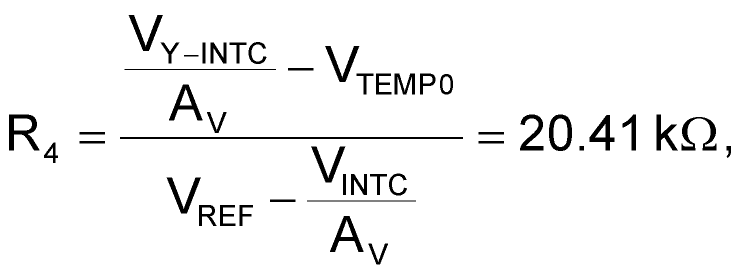
where VY-INTC = 8.5 V is the intersection of the desired temperature curve with the y-axis. For R1 = 301 kΩ, the closest 1% value for R4 is 20.5 kΩ.