Ripple cancellers, also known as ripple-eaters, gyrators, or electronic filters, are useful when a supply needs to be clean but the absolute supply voltage is unimportant. A typical application of these circuits is in class-A power amplifiers. Compared to a linear regulator, they waste less power since they adapt themselves to the input voltage.
There are however some inevitable losses: at the very minimum they have to drop the peak expected ripple voltage, and they also need some operating margin themselves. All of this easily amounts to several volts, leading to a corresponding power waste.
In theory, a purely passive filter could do better, but even with a large inductor, there will always be Joule’s losses. In addition, such a filter would be costly and offer a less than perfect ripple rejection.
This Design Idea combines both methods, and also adds some tricks of its own to achieve a near-perfect, hybrid filter.
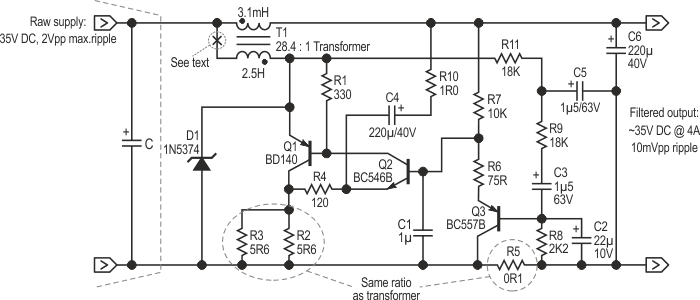
The circuit is based on transformer T1, having its secondary in series with the supply to be filtered. The secondary voltage is therefore subtracted from the input voltage, and if it exactly equals the ripple voltage, perfect cancellation will occur, yielding a pure DC output.
The transformer’s primary is connected to an error amplifier generating a suitable voltage. Basically, two strategies are possible: open-loop and closed-loop. Both can be made to work, and have their specificities: the open loop method samples the input ripple, scales it accurately, and sends it to the transformer. The effectiveness of the cancellation depends on the accuracy of the passive components.
The closed loop circuit samples the output and adjusts the error voltage so as to cancel any ripple. This technique is less reliant on accuracy, but as with any servo system, the accuracy of the process depends on the loop gain, which in turn can cause stability issues. The circuit presented in Figure 1 is of the closed-loop variety.
 |
|
| Figure 1. | Ripple canceller. |
One objection to the use of a transformer is the large DC current flowing through its secondary; normal, ungapped transformers don’t tolerate much DC without saturation, and gapped transformers are much bulkier. Here, the problem is addressed in an elegant manner: the transformer works in compensated mode, the primary receiving exactly the same DC amp•turns as the secondary. To this end, the error amplifier works in class A, and its bias current is servoed to the output current. The current is sensed by R5, and Q1 to Q3 mirror a scaled version through R2 and R3. This ensures that T1 see zero net flux at all times.
Q2 is the error amplifier, and it receives the error voltage on its emitter, via C4.
Stability issues cannot be taken lightly in such a circuit: combining a lot of gain with many reactive components, the circuit has a number of opportunities to turn into an oscillator at a variety of frequencies. The low-frequency compensation is ensured by R9, R11, C5, and C2. C1 takes care of the high frequency department. It has been found in practice that the circuit remained stable without it, but I recommend leaving it in.
Less obvious stability problems can also occur when the input supply is not “stiff” enough. That can happen at light loads, when the internal resistance becomes higher. When the circuit tries to compensate for a drop in the input voltage, the amplifier draws momentarily more current, and if this causes the input voltage to drop further, it results in a positive reaction and instabilities, causing motor-boating. The phenomenon is akin to a right half-plane zero and is almost impossible to compensate away using conventional methods without ruining at the same time the performances of the circuit.
 |
|
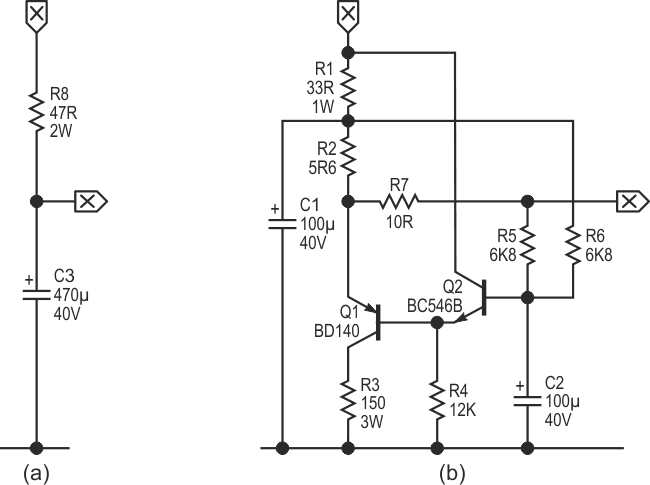
| Figure 2. | An extra filter may be required in some cases. |
In moderate cases, a simple filter in series with the primary may be sufficient (Figure 2a). In difficult cases, an active circuit is required (Figure 2b). This circuit works by duplicating the current drawn by the error amplifier: R2, R5, R6, & R7 are arranged in a bridge, and since R2 is about half the value of R7, Q1 and Q2 try to make R2’s current double R7’s. But C2 delays the action, which means that short-term, the input current is invariable, eliminating therefore the RHP zero. The double-current-law ensures the circuit is never starved dynamically. Note that most of the time, this circuit will not be required.
Implementation notes
The maximum ripple rejection capacity is set by T1’s ratio:

This in turn sets the ratio of R2||R3 to R5.
The transformer’s magnetizing inductance must be large enough to allow the amplifier to develop its full swing. This mandates
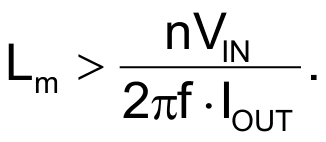
It is advisable to provide some margin with respect to these values, in particular the magnetizing inductance Lm, which should be more than twice the minimum.
Performance
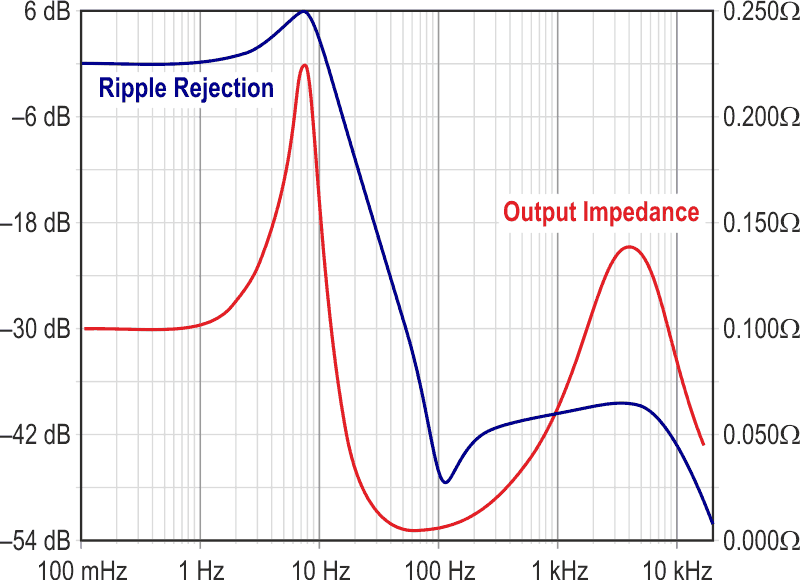
Figure 3 shows the rejection and output impedance curves. Rejection is greater than 40 dB for the pertinent frequency range, with a maximum at 100 Hz exceeding 46 dB. The output impedance too is impressive: the gain of the amplifier helps not only the ripple rejection, but it also actively reduces the output impedance.
 |
|
| Figure 3. | Output impedance and ripple rejection |
The only losses are caused by R5 and the resistance of the transformer’s secondary. They may not be zero, but they are so low that the circuit has a negative drop-out for almost 50% of the time!
This remarkable performance only requires a moderately sized transformer. Let us take an unfavourable example: a 50 V/5 A supply having up to 10% ripple. The secondary/core must have a high enough V•s product to accommodate about 2 VRMS ripple. With the 5 A current, this results in a 10 VA rating. But since the ripple is at twice the mains frequency, this means that 5 VA is in fact sufficient for this heavily rippled 250 W supply.