Circuit improves on temperature measurement

When current pulses with a stable I_HIGH/I_LOW ratio modulate a semiconductor junction, the ensuing voltage difference (for example, ΔV_BE for a bipolar transistor) is a linear function of the absolute (Kelvin) temperature, T. You can use this truism to make accurate temperature measurements. Technical literature has thoroughly covered the relationship (references 1 to 4) and has numerous implementations. This Design Idea suggests some areas for improvement and design variations on the basic idea. The principal equation describing the phenomenon is as follows:

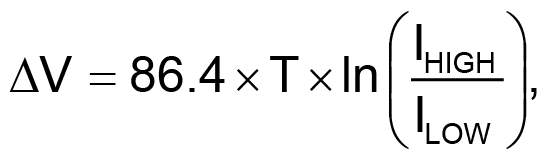
expressed in microvolts. Setting the current ratio I_HIGH/I_LOW = 10 results in ΔV of approximately 200 µV per degree. The key issue in the practice al implementation of the idea is to switch current with a highly stable I_HIGH/I_LOW ratio, which you can do by using a number of discrete components. This Design Idea suggests a digitally controlled and integrated approach (Figure 1).

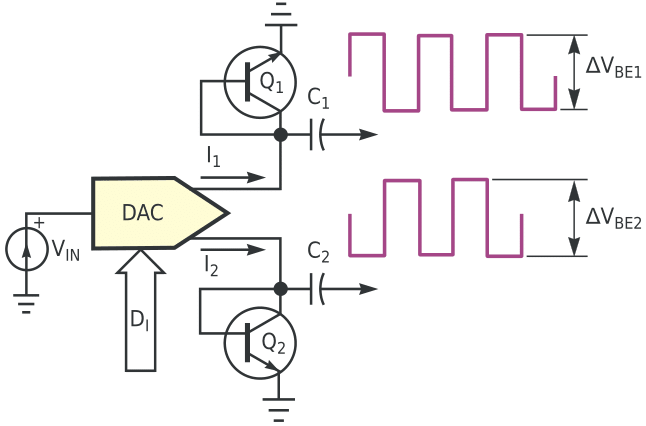
Figure 1.	The DAC modulates transistors Q1 and Q2 with its two current outputs; ΔVBE is a linear function of absolute temperature.

The current switching with a stable I_HIGH/I_LOW ratio, comes from a DAC with current outputs. The typical DAC has two current outputs – a direct I₁ and a complementary I₂. These outputs allow for simultaneous dual-channel temperature measurements. The current ratio I_HIGH/I_LOW is a function of the input digital code, D_I; you could program this code using a microcontroller. Obviously, you can use the circuit for single-channel temperature measurements, by simply ignoring the second output. If you need more than two channels, then use additional DACs or use a multiphase DAC (Reference 5).

The circuit in Figure 1 works as follows: The output currents, I₁ and I₂, are functions of the input digital code, D_I, and the input voltage, V_IN :

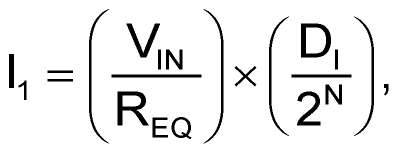
and

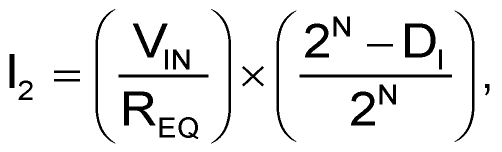
where R_EQ is the equivalent transfer resistance of the DAC, and D_I is the decimal equivalent of the input binary code.

The full measurement cycle consists of two phases, switching codes from D₁ to D₂. Assuming D₁ > D₂, then the current ratio I_HIGH/I_LOW for output I₁ is equal to D₁/D₂. The current ratio for the second output I₂ is equal to

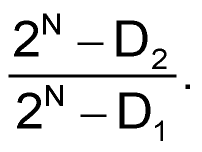
For a 10-bit DAC (N = 10), choosing D₁ = 931 and D₂ = 93, the ratio I_HIGH/I_LOW on both outputs is 10.01, which is close to the “standard” (references 3 and 4). For an 8-bit DAC, these numbers are D₁ = 233 and D₂ = 23, which results in a ratio I_HIGH/I_LOW = 10.13 on both outputs. It’s important that the ratio be substantially immune to variations in the input voltage, V_IN. Thus, any unregulated voltage source is suitable for the circuit. The source needs only short-term stability during the measurement cycle. Besides, many modern DACs integrate on-chip voltage references.

You should note that other I_HIGH/I_LOW ratios are applicable. Moreover, in general, it is unnecessary to have the same current ratios for both outputs. Thus, you could set the sensitivity to different values for the two channels. Higher ratios result in greater sensitivity, but self-heating effects impose certain limitations on I_HIGH, and noise levels set a lower limit on I_LOW. Thus, 100 and 10 µA are typical values for general-purpose bipolar transistors. As most general-purpose R-2R DACs have R_EQ of 10 to 100 kΩ, you should choose the proper value for V_IN (typically 2.5 to 10 V). Alternatively, to obtain the desired I_HIGH, you could use an additional series resistor, R_S (not shown in Figure 1), connected between the voltage source and the DAC input. The R-2R ladder has an equivalent input resistance, R, which does not change with the digital code. With the additional series resistor, the equivalent transfer resistance becomes R + R_S. Note that this series resistor may be of almost any type, because its impact on the current ratio’s accuracy is limited.

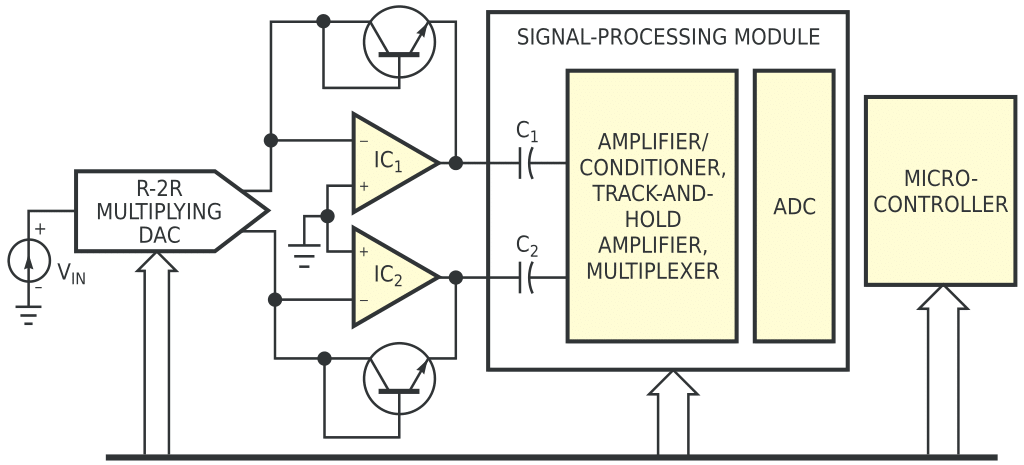Figure 2.	The two op amps, IC1 and IC2, provide virtual grounds for both current outputs of the DAC.

In a practical implementation, you should take into consideration the finite value of V_BE on the DAC’s output, because its variation with temperature could affect the accuracy of the measurement. If the DAC has internal current sources, you can use the circuit of Figure 1 as-is, because the V_BE has a limited effect on the current ratio. In the case of using an R-2R DAC, the circuit in Figure 2 is more appropriate. The two op amps, IC₁ and IC₂, maintain virtual grounds on both current outputs, thus preserving the high accuracy of the current ratios. The rest of the circuit in Figure 2 performs ΔV_BE measurements. You can implement that portion of the circuit by using an amplifier/conditioner, a track-and-hold amplifier, and an ADC controlled by any general-purpose microcontroller. References 3 and 4 offer hints on implementation.

References

1. Belousov, Alexander, “Temperature Measurement Device,” SU Author Certificate 1599674, registered June 15, 1990.
2. Belousov, Alexander, “Temperature Measurement Device,” SU Author Certificate, registered May 1, 1991.
3. Steele, Jerry, “Sense temperatures without Calibration, Electronic Design, May 13, 1998, pg 130.
4. Setton, Joel, “Multichannel temperature measurement system,” Electronic Design, July 10, 2000.
5. Belousov, Alexander, “Multiphase DAC modifies R-2R ladder,” EDN, Jan 18, 1996, pg 87.