Simple sawtooth generator operates at high frequency

Pulse-width-modulation signal-generator circuits often use an analog sawtooth-oscillator function, but it also can be useful in other applications. The inexpensive sawtooth generator in Figure 1 suits use in low-power applications operating at frequencies as high as 10 MHz and beyond and those in which ramp linearity and frequency accuracy are not prominent concerns.

 

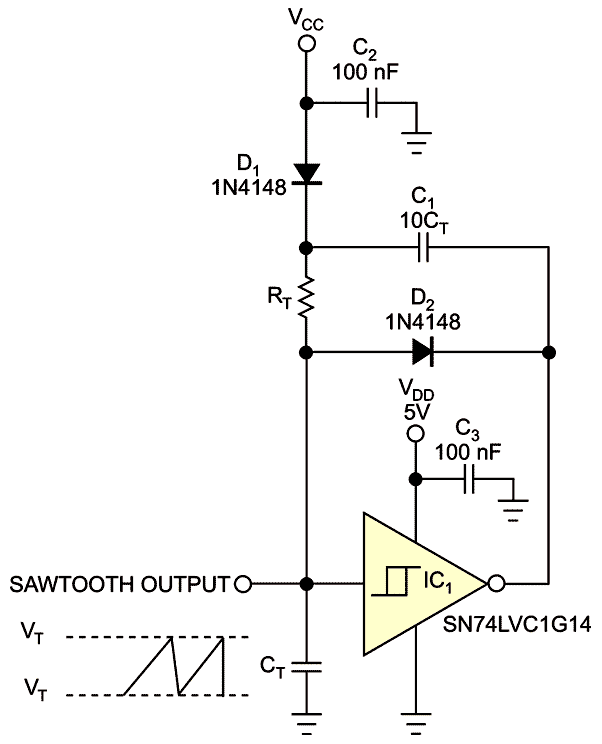
Figure 1.	You can use the CT ramp’s charge and fast discharge to produce a sawtooth. The upper and lower trippoint voltages of the Schmitt trigger limit the sawtooth. See text for the values of VCC, CT, and RT.

The circuit employs a single Schmitt-trigger inverter, which acts as a modified astable multivibrator. The output waveform is the voltage across timing capacitor C_T, which ramps between the lower and the upper threshold voltages of the inverter. Charging the R_TC_T network at constant voltage causes the ramp, so its response is exponential, approximately linear only for the initial part of the exponential rise.

A simple trick to improve ramp linearity is to charge the R_TC_T network with a higher-voltage source. Capacitor C₁, which has a value that is at least 10 times greater than that of C_T, acts as a charge pump. When the gate output is low during the falling edge of the sawtooth, capacitor C₁ quickly charges through diode D₁ to V_CC minus the forward voltage of D₁. Meanwhile, capacitor C_T discharges quickly through diode D₂.

When the falling C_T voltage reaches the Schmitt trigger’s lower trip point, V_T⁻, the gate output returns high. The charge on C₁ drives the cathode of D₁ to the sum of the voltage of capacitor C₁ and the gate’s high output voltage. D₁ becomes reverse-biased, and the R_TC_T network begins to charge to the voltage on C₁, along with the gate’s high output voltage. When C_T reaches the Schmitt trigger’s upper trip point, V_T⁺, the gate’s output returns low, and the cycle repeats.

Ramp linearity is proportional to the sum of the V_CC and V_DD supply voltages. Because V_DD is fixed at 5V, you can improve ramp linearity if V_CC can assume a value higher than that of the inverter. You can estimate the ramp’s nonlinearity error using the following equation:

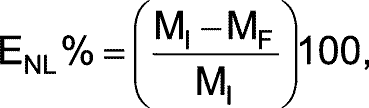
where E_NL% is the percentage of nonlinearity error, M_I is the initial slope of the ramp, and M_F is the final slope of the ramp, and

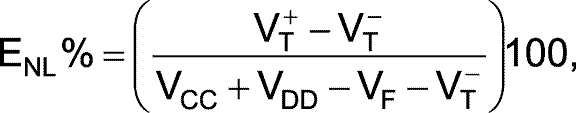
where V_F is the forward-voltage drop across D₁.

The R_TC_T time constant sets the frequency, F_O, of the sawtooth signal. You can estimate the frequency by applying a simple model to the circuit, which neglects the discharge time of C_T and any discharge of C_T, yielding the following equation:

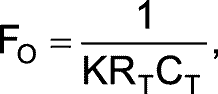
where K is a constant, which the following equation defines:

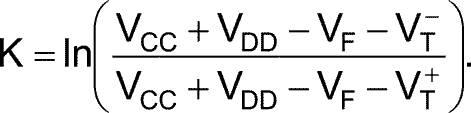
By simulating the circuit with C_T=100 pF and R_T=2.2 kΩ, which agree with the values that the equations theoretically calculated, you can obtain ramp-nonlinearity errors of 28% with both V_CC and V_DD equal to 5V, 18% with V_CC of 10V and V_DD of 5V, and 14% with V_CC of 15V and V_DD of 5V.

The breadboarded circuit has V_DD=V_CC=5V, C_T=100 pF, and R_T=2.2 kΩ. IC1 is a standard dual-in-line, eight-pin 74HC14, which has a maximum propagation delay of 15 nsec versus 4.4 nsec for the SN74LVC1G14 inverter with a V_DD of 5V. The frequency is approximately 12.7 MHz.

C_T should be a low-leakage film capacitor, and its value should be kept low to reduce its charging and discharging of a large amount of energy. Select C_T with a large enough value compared with the gate’s input capacitance and unwanted stray capacitances so that they do not introduce a significant error.

Select R_T with a small enough value that the load impedance, gate input, and stray capacitances do not introduce significant error.

You can use any CMOS Schmitt-trigger inverter to test the circuit. To improve frequency accuracy, however, you should use a fast logic family with low propagation delay and high output current, such as the single-gate SN74LVC1G14 from Texas Instruments.

You should measure the threshold trigger voltages, especially V_T⁻, directly from the circuit under test before using the preceding equations. Quickly discharging C_T to ground through a finite-propagation-delay inverter causes the lower limit of the ramp to reset below the lower threshold, V_T⁻. You can compensate for the resulting error if you use the measured value of V_T⁻, which takes this effect into account.