For at least four decades, dual-slope integrating A-to-D conversion has formed the core of most every digital multimeter and many industrial and instrumentation applications besides. Elegant in its simplicity, a DSADC (dual-slope analog-to-digital converter) employs an analog integrator coupled to a comparator and control logic to accumulate (integrate) the input signal, VIN, for a fixed interval, T1 – comprising the first “slope” – then to switch the integrator’s input to a fixed negative reference, VREF, to ramp the integrand back to zero – the second “slope” – while measuring the time required to do so, T2. The input voltage is thus:
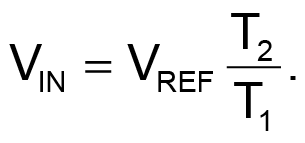 |
(1) |
This Design Idea applies a twist to the familiar algorithm: Simply reversing the order of signal and reference integration results in what I call a reciprocal dual-slope integrating ADC (RDSADC).
Here, VREF is integrated for a fixed interval, T1. Then the integrator input is switched to –VIN, and the time T2 required to ramp back down to zero is measured. Thus:
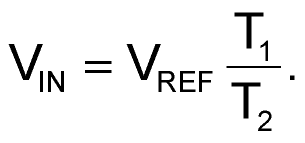 |
(2) |
Given the similar equations, you might reasonably ask: “So what?” So this:
In equation 2, the conversion result is inversely proportional to time measurement T2 and therefore to 1/VIN, and differential calculus tells us that the rate of change of inverses varies, not linearly, but as the square of the inverse of the measured value, i.e.,
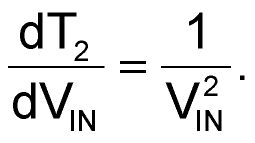 |
(3) |
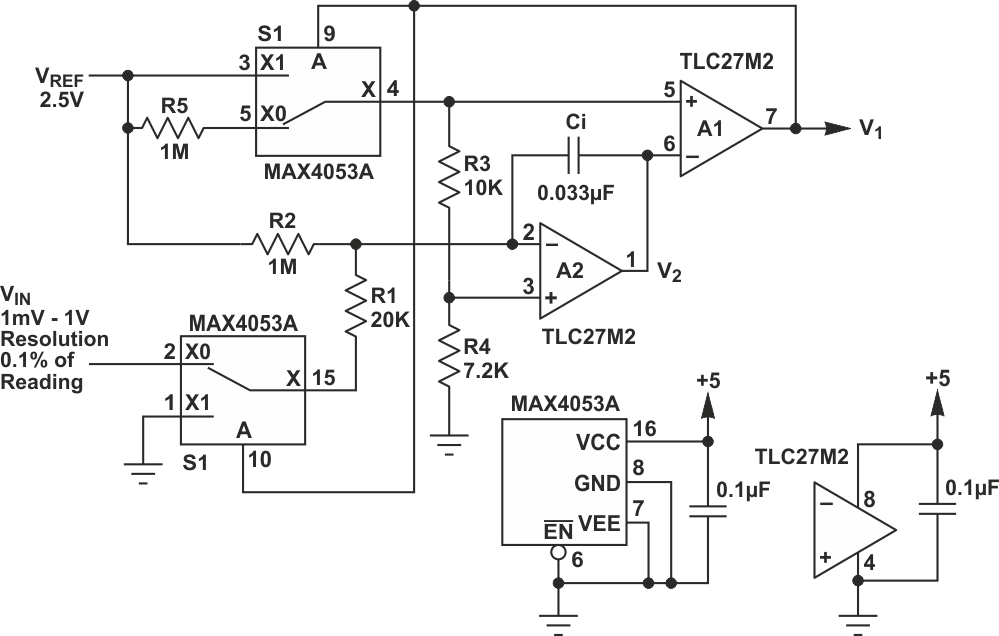
The payoff is therefore a nonlinear conversion measurement that maintains high resolution for low amplitude inputs without any need for auto-ranging of the VIN scale factor. A practical implementation of the RDSADC is shown in Figure 1. It converts inputs in the 10-bit range of 1 mV to 1 V while maintaining a 10-bit resolution at both extremes: 1 mV resolution at VIN = 1 V, and 1 µV resolution at VIN = 1 mV. This translates to a 1,000,000:1, 20-bit dynamic range with only a 15-bit 32k count resolution for T2. In other words, a 20-bit dynamic range is achieved with only a 15-bit count, for a 32:1 improvement in conversion time over a similar resolution conventional DSADC. In fact, VIN can go a bit negative, and all the way to 5 V at reduced resolution.
 |
||
| Figure 1. | RDSADC reverses the usual order of integration to get a big increase in dynamic range. |
|
Here’s how it works:
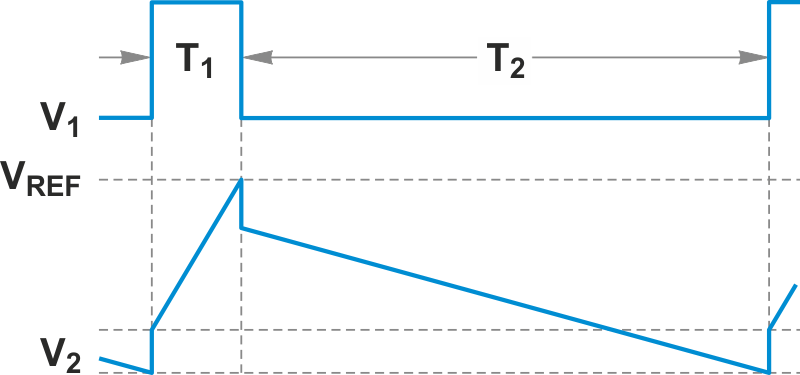
The RDSADC cycle begins with connection of VREF to the “+” input of integrator A2 (pin 3) by S1 through the R4/(R3 + R4) voltage divider, and integration during interval T1, ending when V2 = VREF, switching comparator A1’s output low (Figure 2).
 |
||
| Figure 2. | RDSADC timing diagram: T1: 1 ms (VREF integration) T2: 1-32 ms (VIN integration) Count frequency: 1 MHz Sample rate: 30-500 Hz |
|
S1 then lets A2’s “+” input drop nearly to ground (more on that later), while S2 switches A2’s “-” input nearly to VIN through R1. V2 then ramps downward at a rate nearly proportional to VIN, defining counting interval T2. Arrival of V2 at the low threshold of A1 terminates T2, completing the ADC cycle and beginning a new one, ad infinitum.
About those nearlies: Astute readers will have noticed that during T2, when S1 removes VREF from A1’s “+” input, a 42 mV positive bias is created by R5. The purpose of this bias is to keep A2’s output alive all the way down to the end of the T2 slope despite use of a unipolar power supply.
Also during T2, R2 creates an effective 32 mV bias1) to ensure that T2 remains finite (never more than 32 ms), even when VIN approaches zero. Thus:
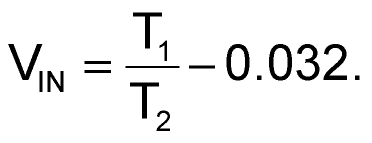 |
(4) |
This idealized arithmetic ignores real-world tolerances like A1 and A2 input offsets, VREF accuracy, and resistor variations, but these imperfections can be easily compensated computationally with a simple two-point VFULLSCALE and VZERO calibration.
1) The 32 mV comes from the R1-R2 voltage-division of the 2.5 V VREF (50 mV), which provides 1.6 µA (32 mV / 20 kΩ) of offset current to the VIN / 20 kΩ input current, minus the “keep-alive” bias provided by divider R3-R5 (18 mV). Hence 50 mV – 18 mV = 32 mV.