PWM circuit uses one op amp

Ferran Bayes

EDN

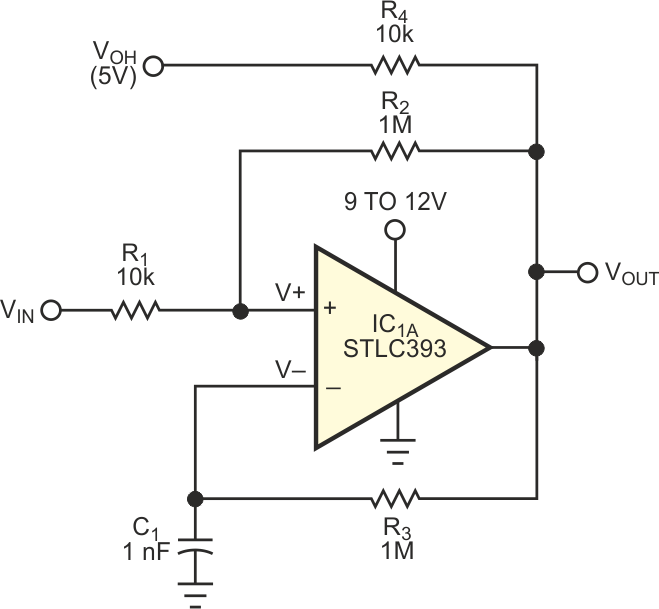
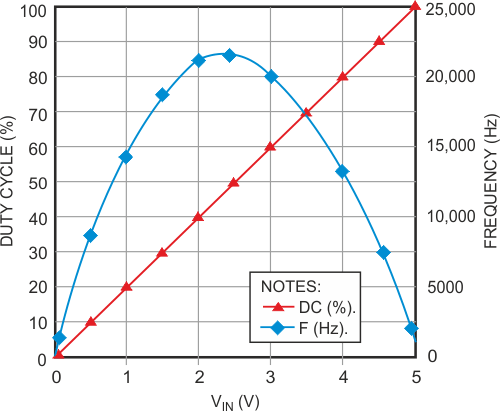
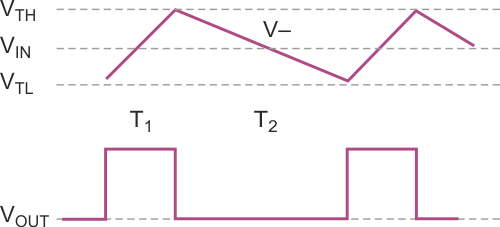
A previous design idea is reminiscent of a similar but somewhat simpler circuit (see [1]). This circuit delivers a rectangular signal with duty cycle varying between 0 and 100% in response to an input signal varying from 0 to 5 V dc (Figure 1). As with the above-mentioned circuit, the frequency is not constant (Figure 2), but the circuit is so simple that it can be useful in certain applications. In response to the hysteresis R₂ provides and the time constant R₃C₁, the comparator delivers the rectangular wave (Figure 3). The voltage V– at the inverting input swings between the two threshold levels, V_TH and V_TL. If you assume that R₂ >> R₁, then V+ is always very close to V_IN. R₃C₁ averages the signal at V_OUT, and the dc voltage at V– is proportional to the duty cycle of V_OUT. The closed feedback loop tries to make V– equal to V+; therefore, the duty cycle at V_OUT is proportional to V_IN.

Figure 1.	This voltage-controlled PWM circuit is simplicity personified.

Figure 2.	Output frequency is a nonlinear function of the input voltage.

Figure 3.	The voltage at the inverting input follows a linear ramp.

The voltage at V_OH determines both the output signal's high level and the full-scale range of V_IN. It can have any value, insofar as it does not surpass the common-mode input range of the comparator. The mathematical analysis of the circuit is easy if we assume that, because V_TH – V_TLis small, we can approximate the exponential charge and discharge of C₁ to assume the characteristic stemming from a constant-current source/sink. During the charging phase, the current is approximately (V_OH – V_IN)/3, so:

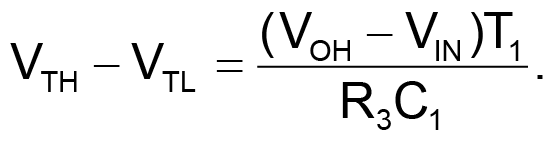
Similarly, during the discharge phase, we can assume the current is V_IN/3, and

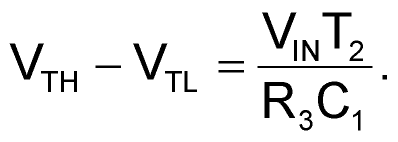
Matching the two equations yields

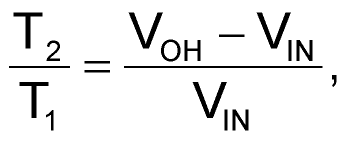
and the duty cycle, D, is

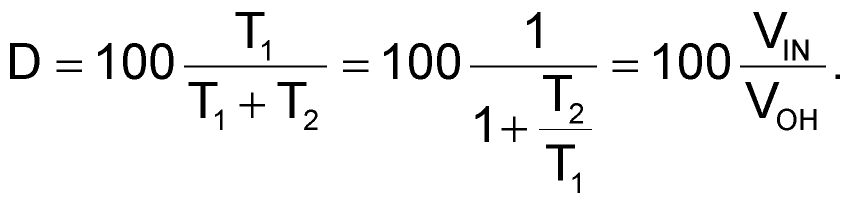
You can see that the duty cycle is directly proportional to V_IN: 0% for V_IN = 0 V and 100% for V_IN = V_OH. Moreover, the duty cycle is essentially independent of the component values, with the constraint that R₂ >> R₁ to keep hysteresis small. An inverse relationship between duty cycle and V_OH can be useful in some applications, so consider V_OH as an additional input. The output frequency follows the relationship

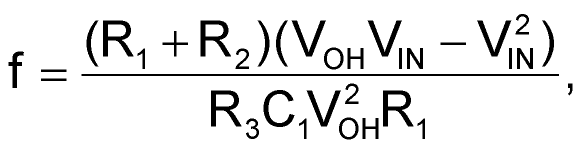
reaching its maximum at V_IN = V_OH/2.

Tests with a TLC393 CMOS comparator and a bipolar LM393 reveal that the TLC393 performs better at low values of V_IN, because of its lower V_OL. Avoid loading the comparator's output; buffer it if necessary, because the loading can degrade the switching levels.

References

Materials on the topic