You can build an analog calculator using a pulse-width modulator (PWM) to perform accurate four-quadrant multiplication and division. While this approach won’t help you ace any math tests, it demonstrates some useful sub-circuits that extend the functionality of the LTC6992 TimerBlox voltage-controlled PWM.
The LTC6992-1 translates a 0-1 V input at the MOD pin into an output with a 0% to 100% duty cycle at a frequency of 3.81 Hz to 1 MHz. A resistor at the SET pin and a resistor divider at the DIV pin control this frequency. In some applications, the LTC6992 will be in the feed-forward path of a closed-loop control system (as in a motor-speed controller), so its 1% typical linearity provides consistent overall loop performance.
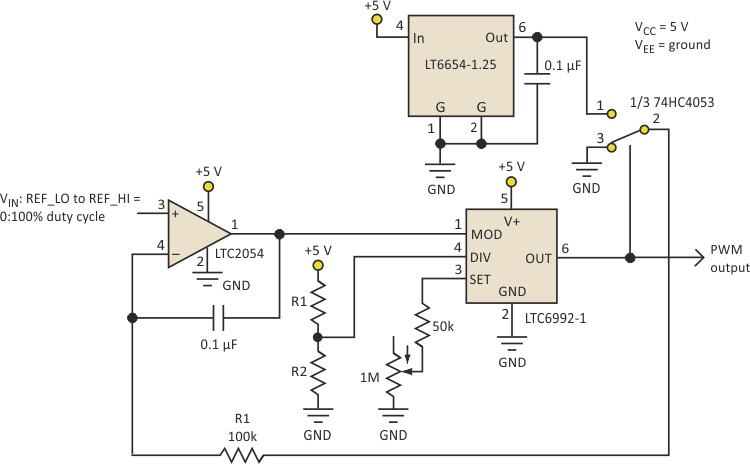
Figure 1 shows a basic linearized PWM generator for applications where accurate PWM is required without an external feedback mechanism. This circuit easily achieves 0.1% PWM accuracy. The output of the LTC6992 controls one section of a 74HC4053 triple single-pole double-throw (SPDT) analog switch whose output is switched between ground and an LT6654-1.25 reference. An integrator compares this signal to the control input. The output duty cycle will settle on a value that equals the fraction of the 1.25-V reference that’s present at the input. The term “fraction” implies that this circuit performs division, as the output PWM duty cycle is VIN/VREF.
 |
|
| Figure 1. | This basic linearized PWM generator, without an external feedback mechanism, can still provide accuracy of 0.1%. |
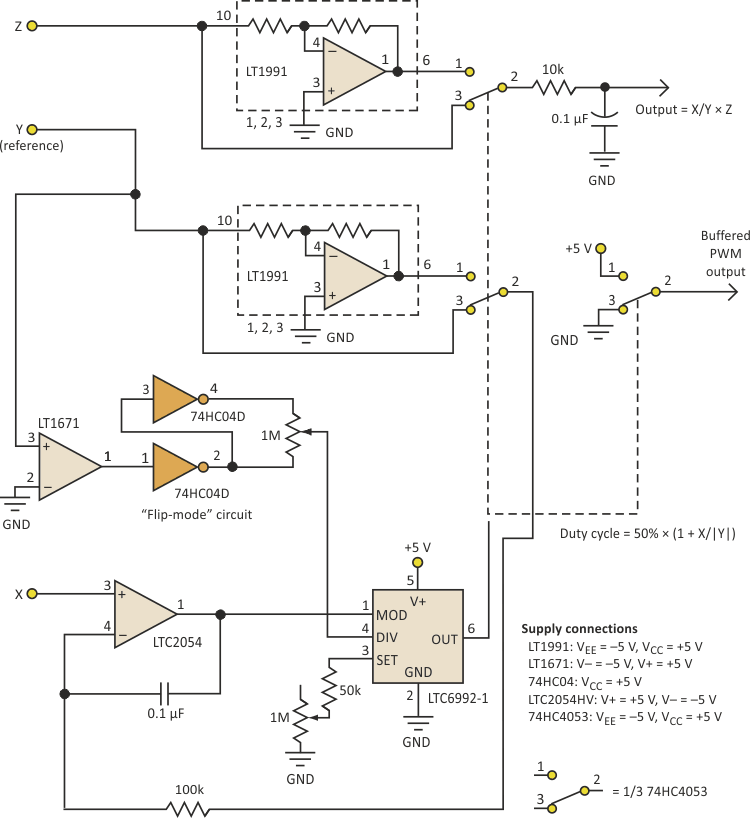
Figure 2 extends this concept, with X as the input (numerator) and Y as the reference (denominator). An LT1991 configured in a gain of –1 provides a precise negative copy of Y, extending operation to four quadrants (positive and negative X and Y), with duty cycle
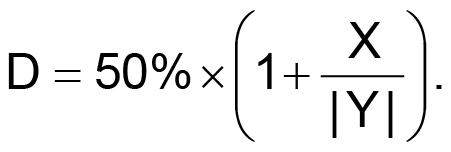
As with any physical realization of division, a zero value for the denominator (Y) will produce an undefined output. A negative voltage applied to the Y input inverts the polarity of the feedback signal to the integrator, which requires another inversion somewhere in the loop to ensure feedback is negative.
 |
|
| Figure 2. | This enhancement to the circuit of Figure 1 extends the analog multiplication/division to all four analog signal quadrants. |
The DIV pin voltage is internally converted into a 4-bit result (DIVCODE), the three lowest bits of which (NDIV) set the frequency division coefficient of the master oscillator. This voltage may be generated by a resistor divider between VCC and GND (See R1 and R2 in Figure 1). The MSB of DIVCODE (POL) determines if the PWM signal is inverted before driving the output. When POL = 1 the transfer function is inverted (a 0- to 1-V input = 100% to 0% duty-cycle output).
The voltage on the SET input sets the current sourced from this pin. The amount of current programs the master oscillator frequency.
The NDIV magnitudes are mirrored around VCC/2, where swapping values in the resistor divider inverts the transfer function while maintaining the same divider value (see the Table 1).
An LT1671 comparator detects the polarity of the Y input and sets the polarity by switching the divider potentiometer’s excitation accordingly, maintaining correct operation. Note that a 10-turn potentiometer works well for experimentation. You could replace it with a fixed resistor once you have selected the desired NDIV.
| Table 1. | DIVCODE programming | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The “Z” input is multiplied by the X/Y quotient by supplying the inputs to another switch with Z and –Z. (Once again, an LT1991 provides precision inversion.) This is a “pulse width/pulse height” multiplier, also with four-quadrant operation.
 |
|
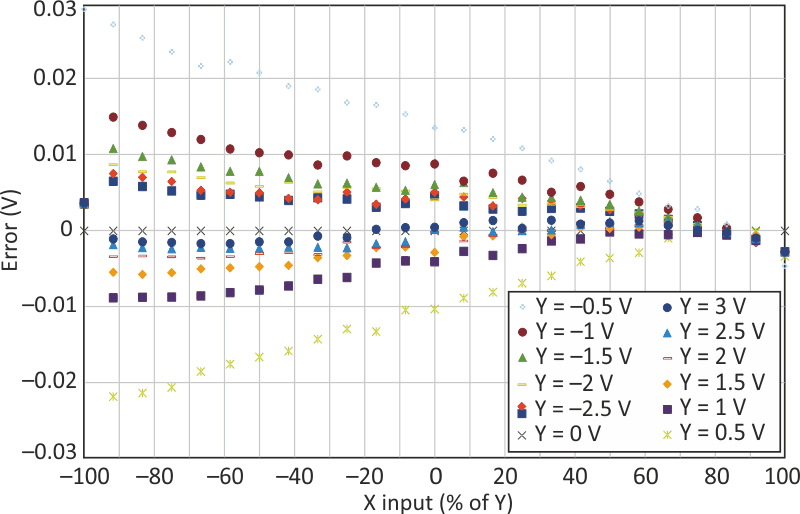
| Figure 3. | This plot of absolute error shows better than 0.1% for large values of Y. |
Figure 3 shows the absolute error of the circuit at a 1.5-kHz frequency, sweeping X from –Y to +Y for values of Y from –3 V to +3 V, while holding Z constant at 5 V. Even with Y at 0.5 V (where error sources are more significant), the worst-case error is about 0.6% and rapidly improves with larger values of Y. Error sources include the 0.04% error of the LT1991, mismatch in switch resistance between its two positions compared with the resistance of the downstream filter's resistance, and the response of the LT1991 outputs to switching transients, whose effect will vary with PWM frequency.