When you design a transformer for any power converter, you face several compromises. You must trade off core size against the number of primary turns and flux density. Another trade-off is the number of turns and winding resistance versus the associated losses. After making these trade-offs, you usually arrive at a good compromise that involves the primary and secondary turns. However, if the converter has more than one output, you face a new set of compromises. For high-power, low-output-voltage converters, the number of secondary turns is often very low. In a forward-converter topology, it is common for a 3.3 V transformer to have one turn in its main secondary winding. This one-turn configuration is ideal for lowering winding resistance and associated power losses.
For this design, the average output voltage is 3.3 V per turn. So, if you need another output from the converter, that output is a multiple of 3.3 V. For a multiple-output power converter, the ratio between the output voltages is often not a whole number (a problem known as “turns granularity”). Referring to this example, if the main output is 3.3 V and the desired auxiliary output is 5 V, two secondary turns yield 6.6 V – a 32% error. A linear regulator could drop 6.6 to 5 V but with the penalty of a power loss. Figure 1 shows an approach to solving the granularity problem if the regulation requirement is not particularly tight (5 to 15%).
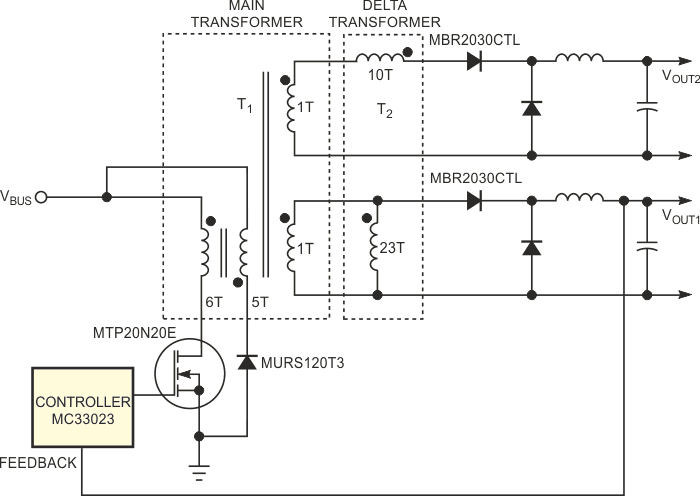 |
|
| Figure 1. | A delta transformer eliminates the problem of turns-ratio granularity. |
Transformer T1 is a normal forward transformer. Each secondary winding has one turn. The control loop regulates the main output, VOUT1, to 3.3 V. The objective is for the auxiliary output to be 5.5 V. With only one secondary turn, that output will also be 3.3 V. Consequently, you need a simple way to increase the voltage. You can add another transformer, T2, dubbed a delta transformer, to the secondaries (Figure 1). The primary of the delta transformer is parallel with the VOUT1 winding, and the secondary of the delta transformer is in series with the VOUT2 winding. This connection has the effect of adding a portion of the main output voltage, VOUT1, to the auxiliary output, VOUT2. (The turns ratio determines the portion.) In the example above, suppose that the main transformer operates at a 50% duty cycle, and assume that the rectifiers have 0.6 V forward voltage drop. Then, the equation relating VOUT1 and the transformer secondary voltage, VT1, during the on time is:
3.3 = (VT1 – 0.6)(0.5) – (0.6)(0.5).
Thus, VT1 = 7.8 V.
Now, you need to solve for the desired total VT (VT2) of the slave output, VOUT2 :
5 = (VT2 – 0.6)(0.5) – (0.6)(0.5).
Thus, VT2 = 11.2 V. VT2 is the sum of the main-transformer secondary voltage and the delta-transformer secondary voltage. The desired delta-transformer secondary voltage is 11.2 – 7.8 = 3.4 V. Because the primary voltage of the delta transformer is also 7.8 V, the turns ratio of the delta transformer must be 7.8/3.4 = 2.3. In this example, you can use 10 and 23 turns for the delta transformer. The main-transformer secondary output delivers current only during its on time, and an internal resistive-voltage drop exists in the secondary output. Therefore, the volt-time product of the main transformer's secondary output is not exactly zero, which is a required condition for the delta transformer's primary to reset. So, you should make the primary winding of the delta transformer resistive to add a small voltage drop in the forward direction or use a small core gap. You can use this approach in all buck regulators to fine-tune an auxiliary output.