The linearity of triangular waveforms makes the triangular- wave generator useful in sweep circuits and test equipment. For example, switched-mode power supplies and induction motor-control circuits often include a triangular-wave oscillator as part of their PWM (pulse-width-modulation) circuit.
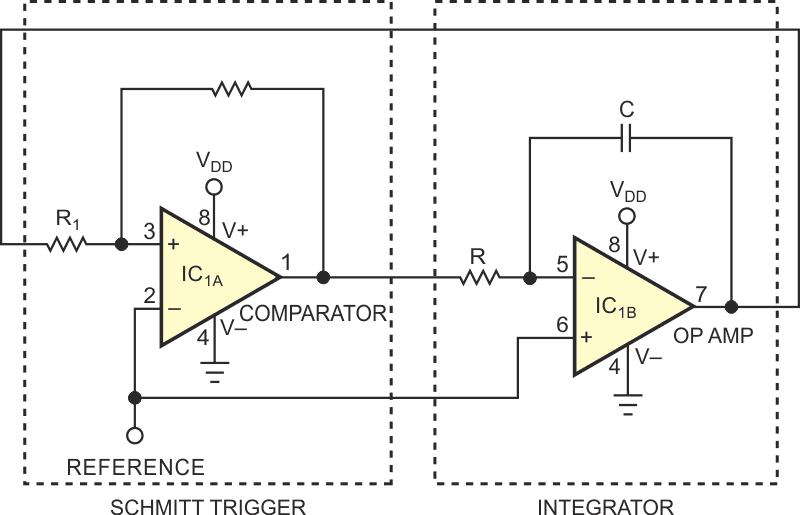
The basic triangular-wave generator includes an integrator for generating the triangular-wave output and a comparator with external hysteresis, such as a Schmitt trigger, for setting the output amplitude (Figure 1). You can implement these components with a MAX9000 IC, which includes a high-speed operational amplifier, a 185-nsec comparator, and a precision 1.23 V bandgap reference.
 |
|
| Figure 1. | The basic triangular-wave generator includes an integrator for generating the triangular-wave output and a comparator with external hysteresis, such as a Schmitt trigger, for setting the output amplitude. |
The integration of a constant current, which you obtain by applying constant voltage across a resistor, produces a linear ramp at the op amp’s output. This output feeds a Schmitt trigger whose output feeds back to the integrator resistor. Abrupt state changes in the Schmitt trigger’s output determine the peak voltages for the triangular-wave output. These changes in turn depend on the input threshold voltages you set for the Schmitt trigger.
Unfortunately for this circuit, the triangular-wave peaks must be symmetrical about the reference voltage you apply to the comparator’s inverting input. To generate a triangular wave from 0.5 to 4.5 V, for example, you must provide a reference voltage of (0.5 V + 4.5 V)/2 = 2.5 V.
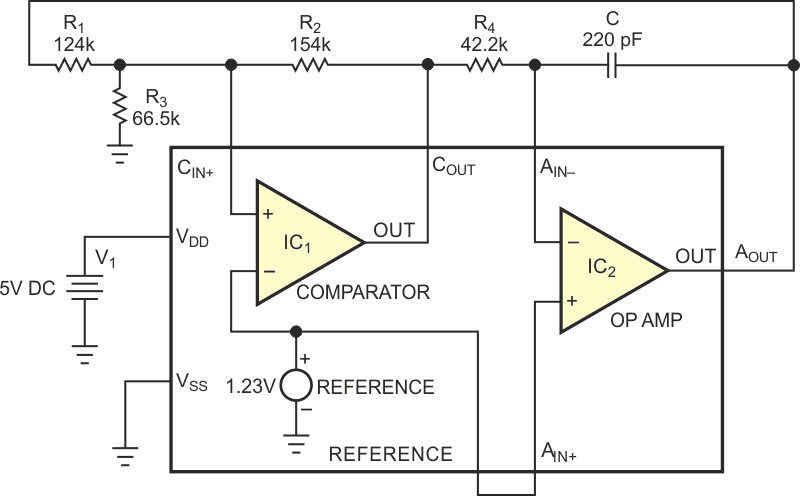
It would be preferable to set this voltage range independently of the standard bandgap-reference voltage available, 1.23 V. You can achieve this flexibility by adding resistor R3 to the hysteresis network in a single-IC version of the circuit (Figure 2). R3 lets you set the triangular-wave peaks independently of the reference voltage.
 |
|
| Figure 2. | A triangular-wave generator employs an IC that includes an op amp, a comparator, and a bandgap reference. |
To build the Schmitt-trigger comparator, you first select R2. The comparator’s input-bias current at CIN+ is less than 80 nA. To minimize the error this current causes, the current through R2,
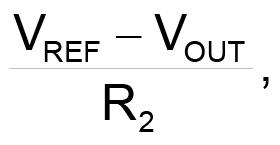
should be at least 8 µA. R2 requires two equations, corresponding to the two possible comparator-output states:
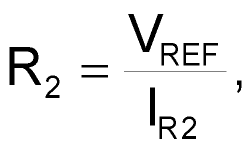
and
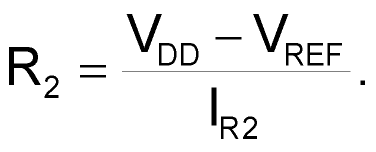
Use the smaller of the two resulting resistor values. For example, if the supply voltage is 5 V, the reference voltage is 1.23 V, and the reference current is 8 µA, the two R2 values are 471.25 and 153.75 kΩ, so this circuit uses the standard value of 154 kΩ.
Next, select R1 and R3. During a rising ramp, the comparator output is logic low (VSS). Similarly, the comparator output is at logic high (VDD) during a falling ramp. Thus, the comparator must change state according to the required peak and valley points of the triangular wave.
Two simultaneous equations result when you apply nodal analysis at the noninverting input of the comparator and solve for these two thresholds:
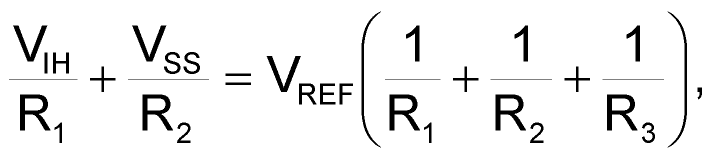
and
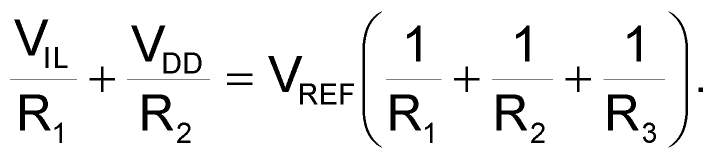
In this example, the voltage range of the triangular wave is 0.5 to 4.5 V. You therefore substitute a value for VIH of 4.5 V, VIL of 0.5 V, VDD of 5 V, and VREF of 1.23 V into the above equations to obtain a value of 124 kΩ for R1 and 66.5 kΩ for R3.
You can now design the integrator. Considering the comparator’s two possible output states, the magnitude of current flowing through R4 is:
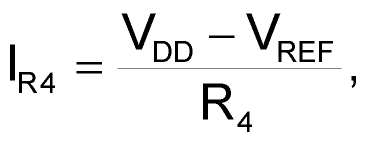
or
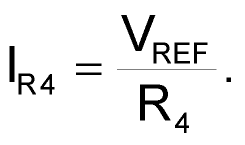
The op amp’s maximum input-bias current is 2 nA. To minimize error, therefore, the current through R4 must always be greater than 0.2 µA. This constraint implies that R4’s value is less than 6.12 MΩ.
The triangular-waveform frequency is:
For this example, the frequency is 25 kHz, the output voltage is 4 V p-p, or 0.5 to 4.5 V for a triangular wave, and the reference voltage is 1.23 V. Solving for the resulting time constant, R4C = 9.27 µsec. Select a capacitance of 220 pF and a value of 42.2 kΩ for R4.
The resulting output should match the desired frequency, provided that the op amp is not slew-limited. Because the feedback capacitor charges or discharges with a constant current, the output signal’s maximum rate of change is:
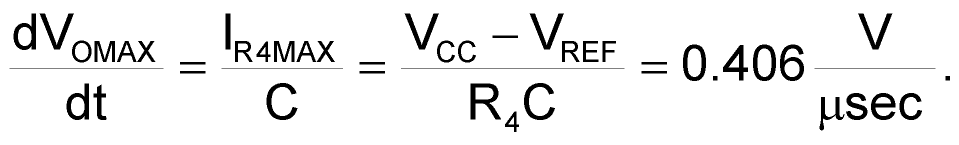
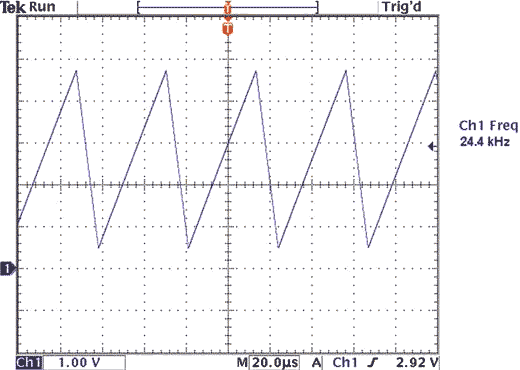
To provide a margin against process variations, the op amp’s typical slew rate should be 40% higher than the maximum rate of change of the output signal – 0.56 V/µsec or greater in this case. The op amp’s slew rate is 0.85 V/µsec, which is therefore adequate for this 25-kHz waveform (Figure 3).
 |
|
| Figure 3. | The op amp’s slew rate is 0.85V/µsec, which is therefore adequate for this 25-kHz waveform. |
Reference
- Terrell, David L, Op Amps: Design, Application and Troubleshooting, Butterworth-Heinemann, 1996.
