In switch-mode power converters, peak current control is very popular because of its inherent current limitation and ease of control. However, if the duty cycle is higher than 50%, there is an instability problem.
Some background: The up-slope of the current is
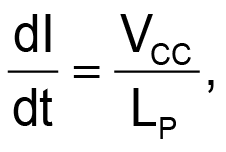
where VCC is the supply voltage and LP the inductance of the transformer or output inductor.
The down slope is
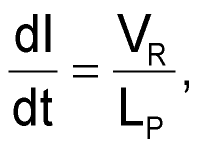
where VR is the reflected secondary voltage to the primary;
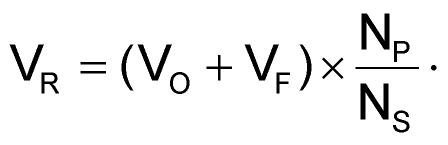
So the up slope depends on the input voltage and the down slope is constant. The duty cycle is:
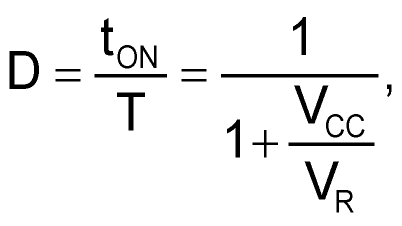
The following examples assume a flyback converter, but a buck or forward converter has the same problem.
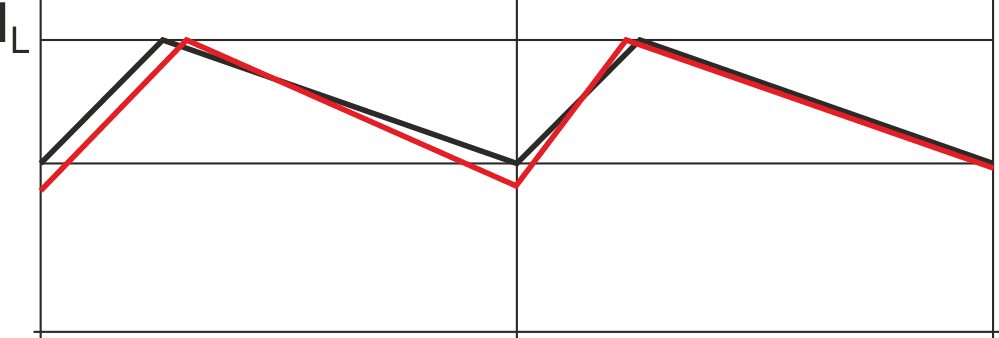
In Figure 1, D < 0.5, that is, VCC > VR. The black waveform is the theoretical current in the inductance (inductor or transformer primary). If there is a small perturbation of the current, as shown in the red waveform, the peak current limit corrects the error, as seen in the figure. The system is inherently stable.
 |
|
| Figure 1. | Stable operation. |
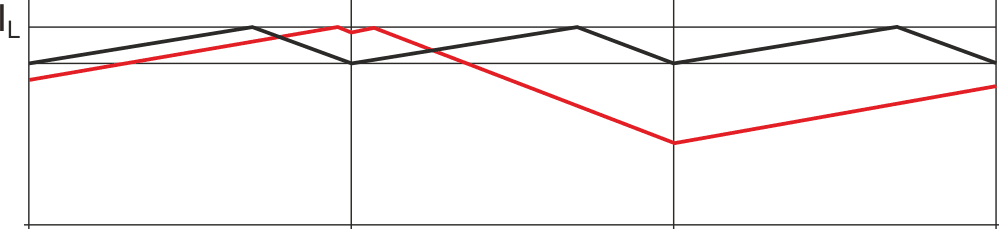
In Figure 2, the same waveforms are shown when VCC < VR, or D > 0.5. Now the perturbation in the current (in red) causes a dramatic change in the duty cycle and the average current. The system is absolutely unstable. If we draw the waveforms for D = 0.5, it is easily seen that the current error remains the same in the following cycles; we are at the boundary of the instability.
 |
|
| Figure 2. | Unstable operation. |
 |
|
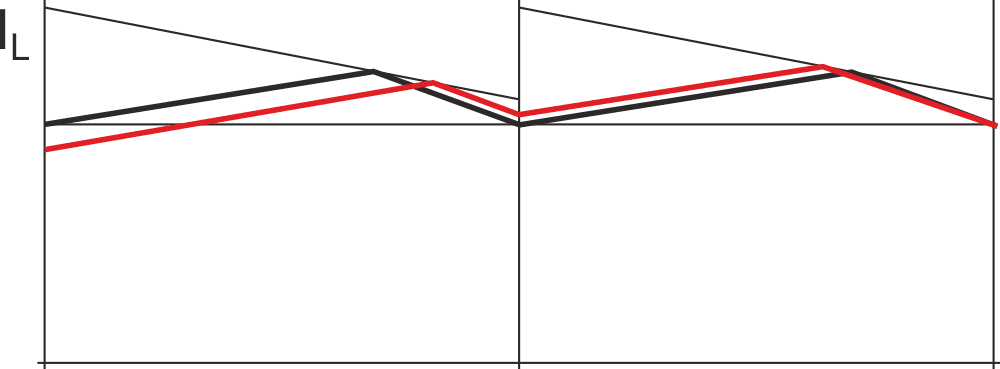
| Figure 3. | Ramping current limit. |
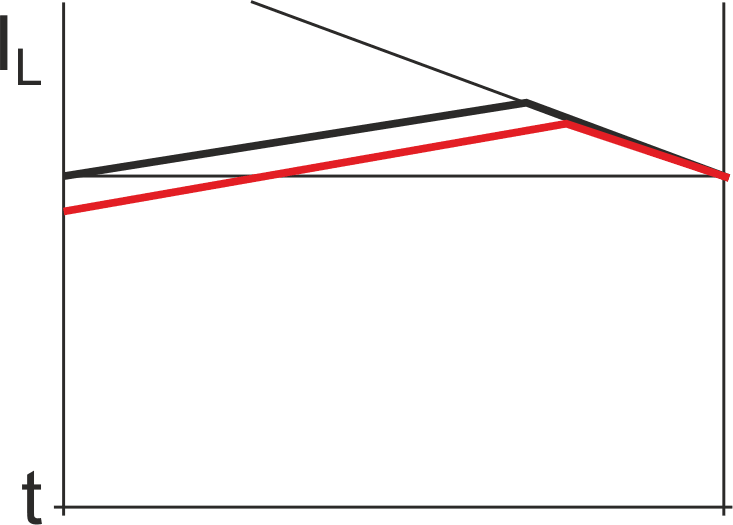
To remedy the problem, instead of comparing the peak current with a fixed value, we compare it with a ramp, as shown in Figure 3. As we can see, there is a dramatic improvement: the stability is now as good as when the duty cycle is under 0.5. Figure 4 shows that if the reference ramp has the same slope as the down current ramp, the recovery occurs in a single cycle.
 |
|
| Figure 4. | Ramping current limit with the same slope as the inductive down current. |
However, too much slope compensation makes the converter behave more like a voltage mode converter than a current mode one. If the slope of the reference ramp is 50% of the current slope, we are at the limit of instability. Thus, a practical slope for the reference ramp is between 50% and 100% of the current ramp; 75% is a good choice. This method of adding the reference ramp is called “slope compensation”.
The added ramp has benefits even with buck, forward, or flyback converters working at duty cycles lower that 50%. If the inductance is high and the current ripple is low, noise may cause false turn-offs. The added ramp stabilizes the converter, and a small amount may be enough. A problem with the peak current limit is that the average current changes with the duty cycle. If the slope compensation is 50% it can be shown that the average current does not change with the duty cycle, and the current control loop is improved. However sub-harmonic oscillations can occur when the duty cycle approaches 100%.
Normally it is not possible to access the reference voltage of the IC controller. The simpler way is to add a ramp to the input current signal: a positive ramp there will have the same effect as a negative ramp in the reference voltage. The standard method is to use the ramp of the oscillator of the PWM controller, as shown in Figure 5.
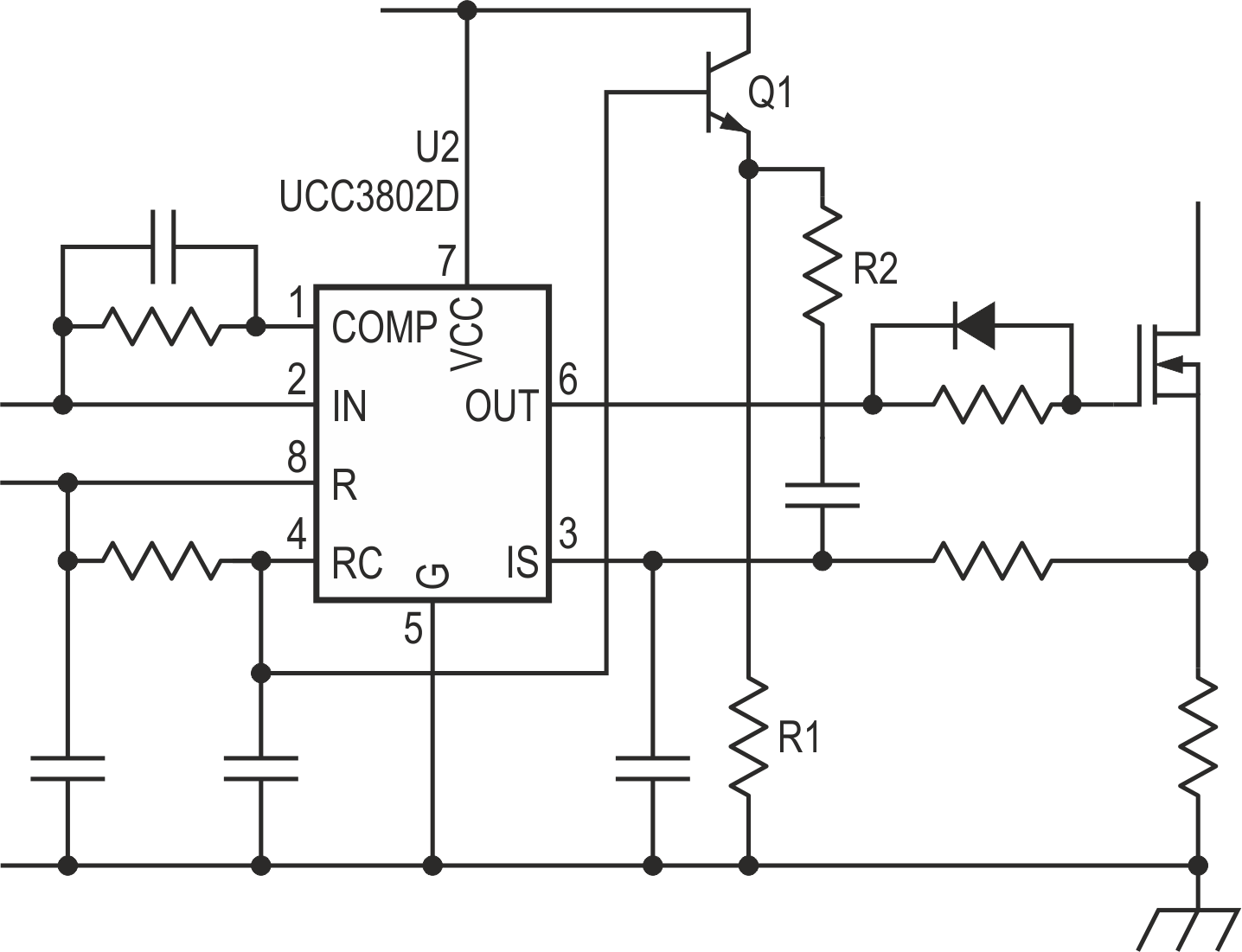 |
|
| Figure 5. | Typical slope compensation. |
This system has two drawbacks:
- Not all the controllers have the oscillator ramp accessible.
- The value of R1 has to be quite low (R1 << R2, e.g., R1 = 0.1 × R2), so in spite of Q1 buffering the resistor, the oscillator circuit is loaded and the frequency can be impaired.
The Design Idea in Figure 6 is free of these problems. It works with any controller without relying on its oscillator circuit.
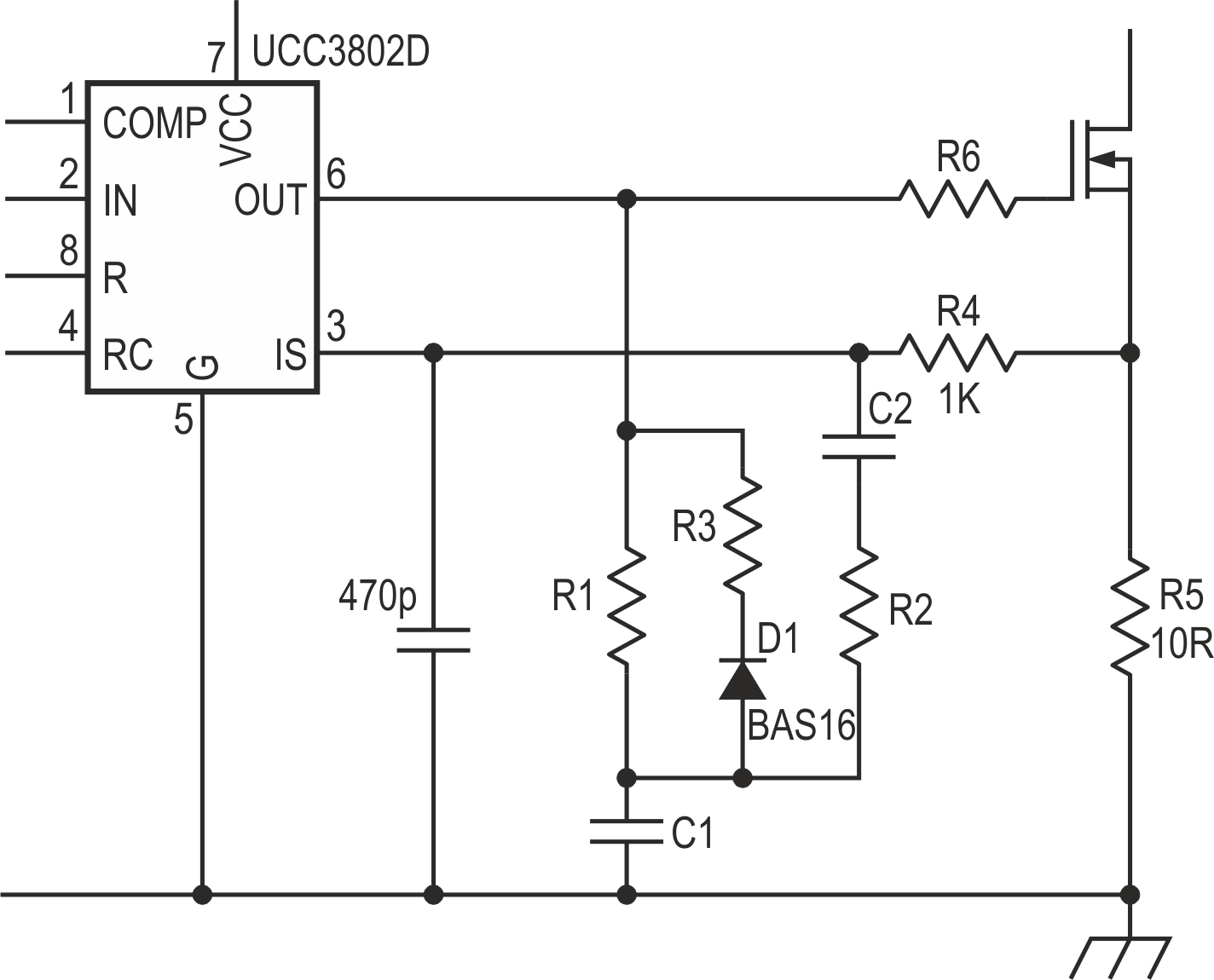 |
|
| Figure 6. | Slope compensation that works for any controller. |
When the output to the gate is high, the ramp goes up as R1 charges C1. When the gate output goes down, C1 is discharged through D1 & R3. The amount of slope compensation is set by R2.
A practical example will help to understand the circuit and calculate the values. The example is a 10 W 12 V continuous mode flyback converter. It has to work from 135 to 390 VDC input.
Primary inductance is 33 mH, IMAX = 0.1 A, so R5 = 10 Ω for a 1 V IS threshold.
The reflected secondary voltage to the primary is
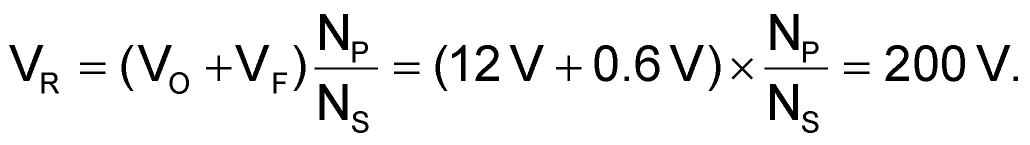
(Turns ratio is 16:1). Switching frequency = 100 kHz (T = 10 µs).
To get a fairly linear ramp, its maximum voltage can be selected to be 1/3 VCC; that is, if VCC = 12 V, a reasonable peak voltage is 4 V. Then the ramp amplitude is 4 V – 0.6 V = 3.4 V.
Calculate the maximum duty cycle:
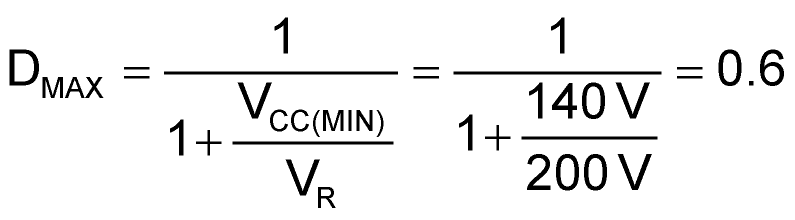
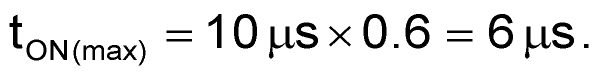
The slope of the ramp:
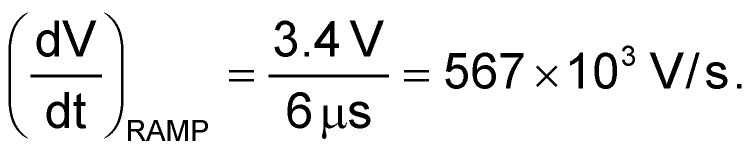
The down slope of the primary current:
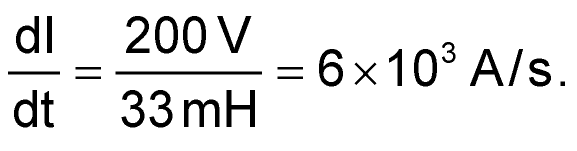
The slope of the voltage in R5:
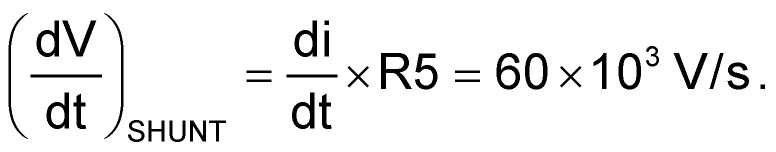
Calculate R2 for 75% slope compensation:
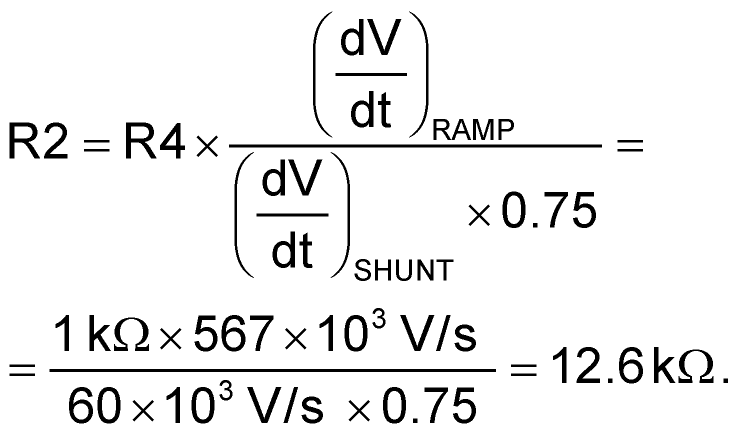
The next step is to find the values for R1 and C1, with R1 << R2. We have to use the charging capacitor equation:
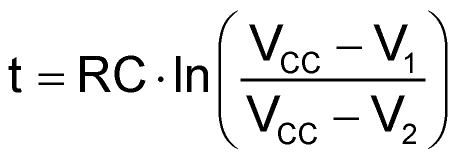
to get suitable values for R1 and C1. In the example, t = 6 µs, VCC = 12 V, V1 = 0.6 V, V2 = 4 V, so the result is RC = 17 µs.
A good choice is C1 = 22 nF and R1 = 750 Ω.
The discharge resistor R3 can be as small as possible while keeping the peak D1 current within its limits; R3 × C1 << tOFF. In our example D1 is a BAS16 and R3 = 47 Ω, tOFF = 4 µs, R3 × C1 = 1 µs.
C2's reactance has to be much lower than R2; C2 = C1 is a convenient choice.