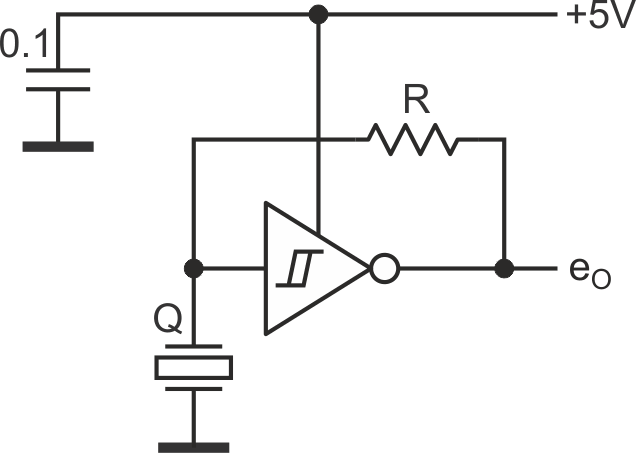
The circuit in Figure 1 seems utterly simple but demonstrates unusual behavior. It produces an almost square wave of odd-integer quartz harmonics, including its main frequency.
 |
|
| Figure 1. | A simple circuit that produces an almost square wave odd-integer of quartz harmonics. |
You can determine the output frequency of the circuit (FO) simply by varying a resistor’s value.
The circuit uses shock excitation for the resonance oscillation of the quartz. In contrast to well-known oscillators, the circuit explores feedback from its highly nonlinear output providing the shock excitation of the quartz resonator which synchronizes the circuit oscillation.
One potentially strange choice was to use a Schmitt trigger as an active element, albeit this trigger is far more helpful than an ordinary inverter; in this case it also ensures the unusual abilities of the circuit.
The output square wave of Schmitt trigger contains only components of odd-integer harmonic frequencies (of the form 2π(2k–1)×f).
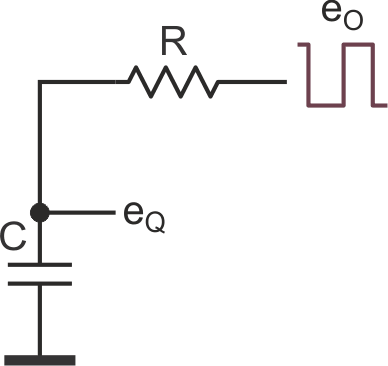
Hence, filtering out the undesirables with the help of LPF RC (look at the equivalent circuit on Figure 2) can provide a quite good excitation for the quartz. (Here C is the common capacitance associated with the quartz node: a parasitic capacitance plus capacitances of the trigger input and the quartz itself.)
 |
|
| Figure 2. | A simple circuit that produces an almost square wave odd-integer of quartz harmonics. |
Assuming the rising threshold VT1 and the falling threshold VT0 are symmetrical (the case of 54HC14), the frequency of a free-running Schmitt trigger RC oscillator can be found by the approximately by equation:
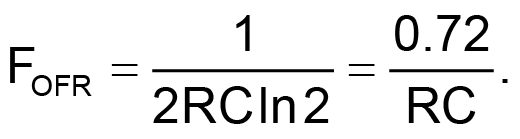
To make the synchronization possible, this free-run frequency must be slightly less than the target frequency.
Note: if this condition is not held, the circuit can oscillate on a stray combination of sub-harmonics of the quartz, or any unrelated frequency determined mainly by RC. The question of the phase noise of such an oscillator is also open.
The circuit may be less useful for higher frequencies since a higher frequency means lower value of R and therefore more heavy shunting of the resonator by this resistor. The lower values of R also distort our simple model of a square wave oscillator.
But it is well suited for rather low quartz frequencies, it was used for frequencies in the range from 32 kHz to 1 or 2 MHz.
For instance, with FQ = 100 kHz the values of R in range 150k to 250k correspond to the main frequency (100 kHz), R from the range 85k to 40k gives the 3rd harmonic (300 kHz), values from the range 65k to 75k will give 5th harmonic (500 kHz) and so on. Surely, all these values are given as a guide for the case of 54HC14 and EDD = 5 V.