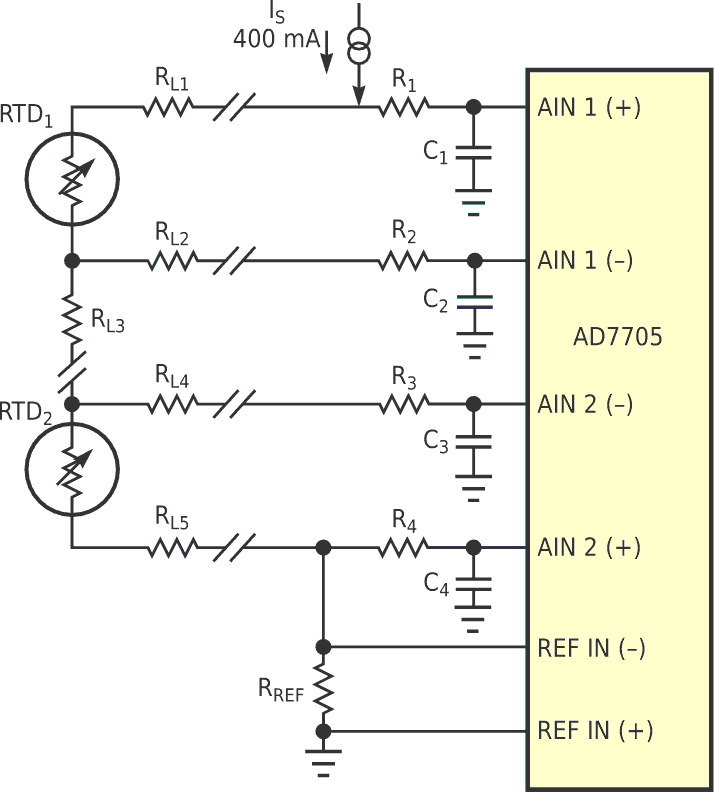
You sometimes need to measure the differential temperature between two points in a system to a greater accuracy than that required in measuring the absolute temperature at either of the individual points. Differential-temperature measurement is necessary, for example, in monitoring heating-energy consumption in an apartment. Hot water enters from one pipe, circulates around the apartment through the radiators, and exits through a second pipe. Billing depends on the temperature differential between the entry and exit copper pipes, so absolute temperature is irrelevant. One way of measuring is to attach an RTD (resistance-temperature detector) to each pipe as it enters or exits the apartment and to take the voltage difference across the two RTDs. To ensure that the measurements are truly relative, you must wire the RTDs in series and excite them with the same current source, IS (Figure 1). The same excitation current also flows through the reference resistor, RREF, and generates the voltage reference for the ADC. Hence, the entire circuit is ratiometric. Therefore, both the current source, through, and the reference resistor need not be particularly stable over temperature for the circuit to operate properly. The circuit is also tolerant of ohmic drops in the connections to the three-wire RTDs.
 |
|
| Figure 1. | This ratiometric differential-temperature measurement system eliminates ohmic wiring drops as sources of errors. |
Channel 1 of the AD7705 reads an input voltage equal to IS RRTD1 + IS RL1. Channel 2 reads an input voltage equal to IS RRTD + IS RL5. RL1 and RL5 represent the wiring resistances between the local electronics and the remote RTD elements. You should wire the RTDs such that RL1 = RL5. Using software, subtract the ADC’s Channel 1 reading from the Channel 2 reading. The ohmic drops cancel, leaving the differential temperature as the only remaining term. The inter-RTD wiring resistance, RL3, does not appear in the equations and, therefore, has no effect. The input impedance of the AD7705 is very high, so essentially no current flows through RL2 and RL4. The RC combinations act as lowpass filters that attenuate high-frequency noise that the wiring picks up. This filtering function is especially important with RTDs that are remote from the AD7705 and related measurement electronics.
The RTDs give rise to a certain source of errors. Consider a common 100 Ω platinum RTD with a resistance coefficient of 0.003 Ω/Ω/°C. This type of sensor, the European PRTD, is the most common RTD sensor. It is available in accuracy-tolerance classes A and B (or DIN A and DIN B), which specify both the initial accuracy at 0 °C and the interchangeability over the operating range. Class A specifies ±(0.15+0.002|t|), and Class B specifies ±(0.3+0.005|t|), where t is the specified interchangeability temperature. You can buy two Class A, 100 Ω, platinum RTDs from the same manufacturer and find that one is reading 0.2 °C high at 25 °C and the other is reading 0.2 °C low at 25 °C. This difference represents an apparent 0.4 °C difference before you even commission the measurement system. To combat this initial error, you must either request a matched pair of RTDs from the manufacturer or calibrate out this difference at the time of installation. For instance, some sensor manufacturers sort PRTDs into tolerance groups with maximum Δt of ±0.05 °C over 0 to 100 °C. Alternatively, you can easily calibrate out the error by using the AD7705’s separate gain and offset registers for the two channels.
The AD7705 specifies integral nonlinearity at 14 bits or better. However, the ADC measures the two inputs with 16 bits of peak-to-peak resolution. All this resolution is useful, because the ADC has the same linearity for either channel, whatever that resolution may be. This premise assumes that the gain of the ADC’s internal PGA does not change between channels. Changing channels via the internal multiplexer does not contribute any additional error sources. Thus, differential-temperature measurements have a resolution of 14 bits or better.