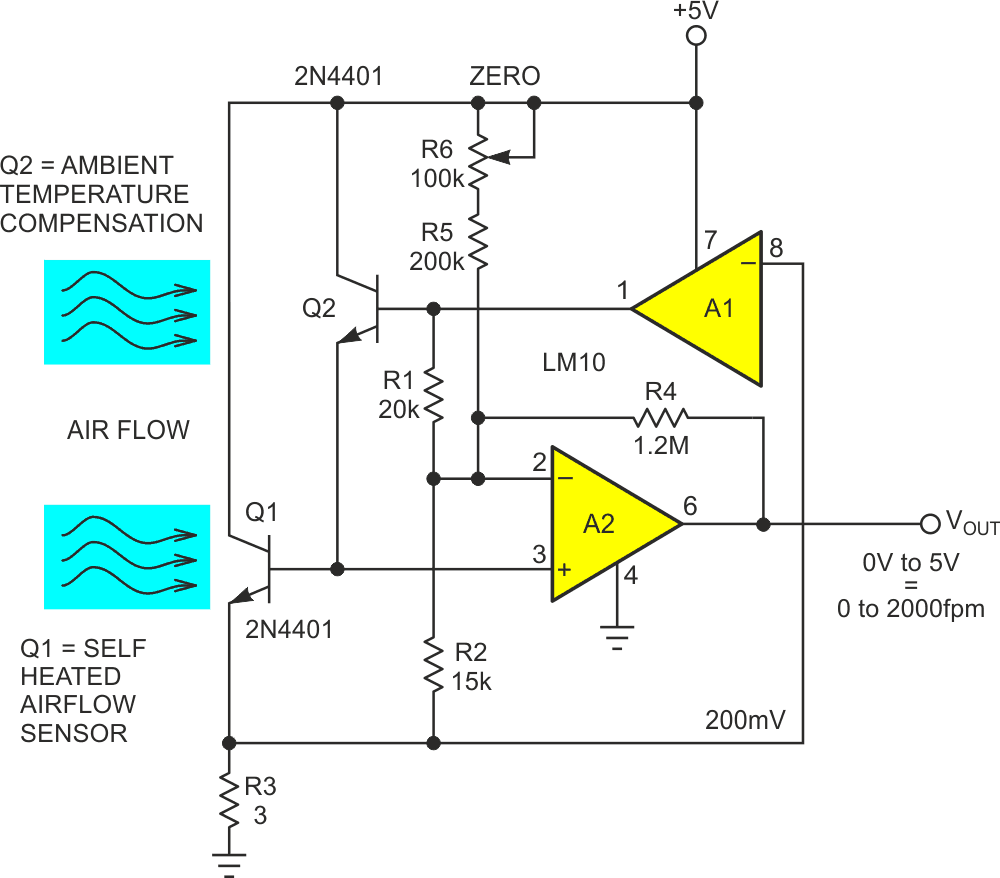
Self-heated transistors used as thermal air flow sensors are a particular (obsessive?) interest of mine, and over the years I must have designed dozens of variations on this theme. Figure 1 illustrates one such topology seen here (Reference 1) before. It connects two transistors in a Darlington pair with Q2 serving as an unheated ambient thermometer and Q1 as the self-heated airflow sensor. Reference amplifier A1 and current sense resistor R3 regulate a constant 67 mA = heating current = 333 mW @ 5 V heating power.
 |
|
| Figure 1. | Typical self-heated transistor thermal airflow sensor. |
This heat input raises Q1’s temperature above ambient by 64 °C at 0 fpm air speed, cooling to 24 °C at 1000 fpm as shown in Figure 2.
 |
|
| Figure 2. | Thermal sensor temperature versus air speed. |
As shown in Figure 2, the relationship between the airspeed and cooling of the self-heated transistor sensor is highly nonlinear. This is an inherent characteristic of such sensors and causes the sensor temperature versus air speed signal to be equally nonlinear. Consequently, even relatively small power supply instabilities, that translate % for % into instability in sensor temperature rise, can create surprisingly large airspeed measurement errors.
Clearly, anything less than perfect power supply stability can make this a problem.
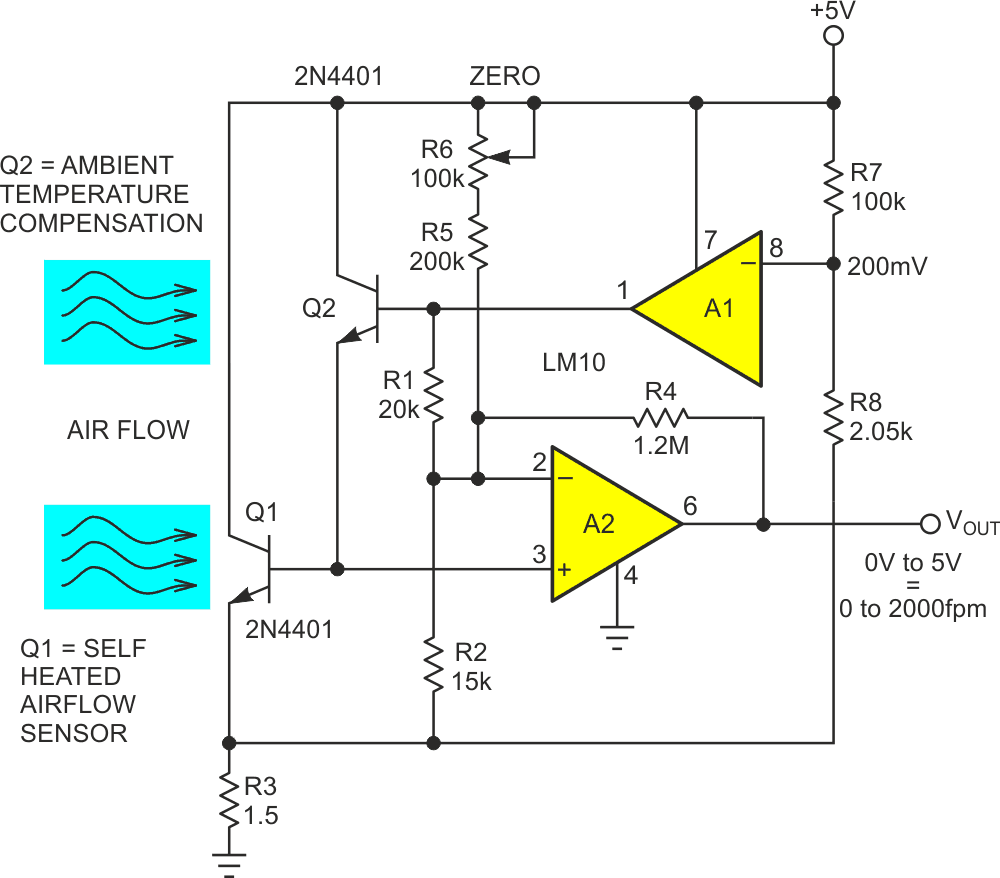
But Figure 3 offers a surprisingly simple and inexpensive fix consisting of just two added resistors: R7 and R8.
 |
|
| Figure 3. | Added R7 and R8 establish an instability-cancelling relationship between heating voltage V and heating current I. |
The added Rs sum feedback from current sensing R3 with heating voltage source V. Summation happens in a ratio such that a percentage increase in V produces an equal and opposite percentage decrease in current I, and vice versa. The result is shown graphically in Figure 4.
 |
|
| Figure 4. | Sensor temperature versus supply voltage where: Blue = heating voltage V and (uncorrected) power; Red = heating current I; and Black = I×V = heating power / temperature. |
Note the null (inflection) point at 5 V where heating is perfectly independent of voltage.
Here’s the same thing in simple nullification math:
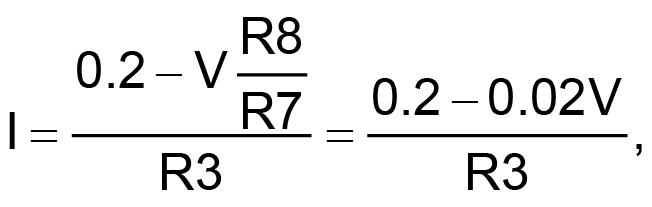
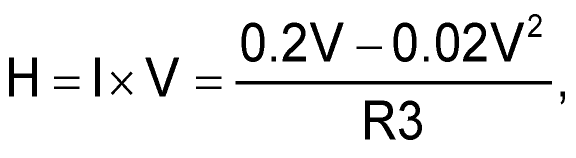
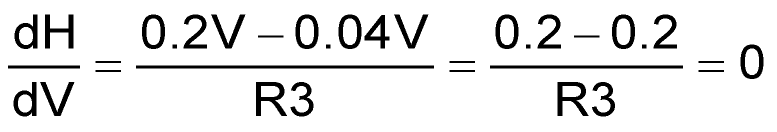
@ V = 5 volts
dH = –0.01%
@ V = 5 volts ±1%.
Note the 200:1 stability improvement that attenuates a ±1% variation in V down to only –0.01% variation in heating power and therefore temperature.
Problem solved. Cheaply!
Reference
- Woodward, Stephen. “Self-heated Darlington transistor pair comprises new air flow sensor.”