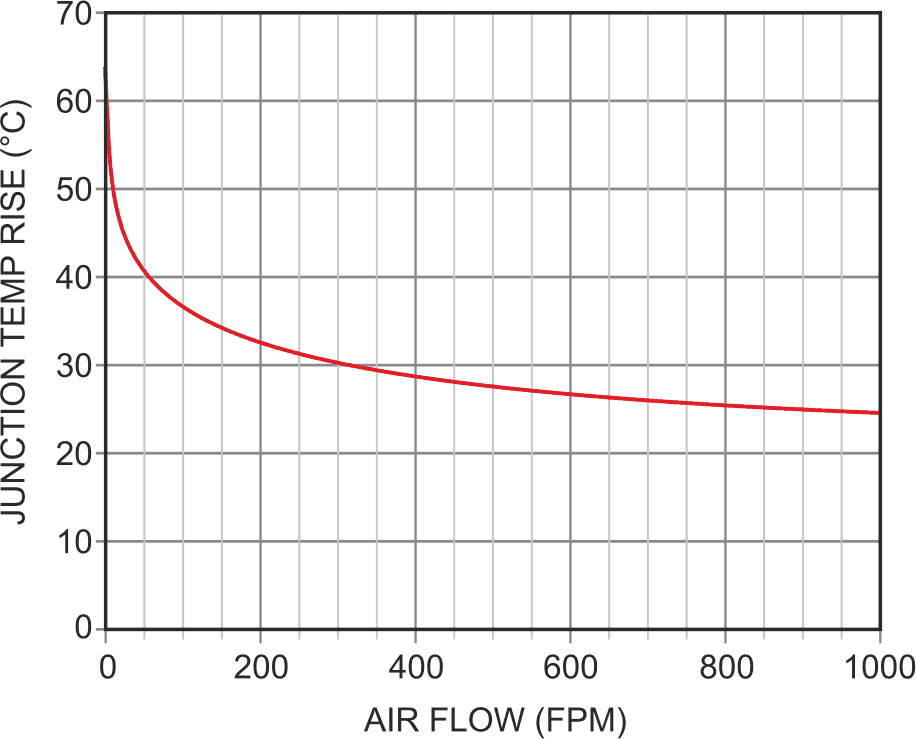
Self-heated thermal airflow sensors are simple, cheap, rugged, and sensitive. However, they exhibit an airspeed to sensor temperature response (King’s Law) that is very nonlinear, as shown in Figure 1.
 |
|
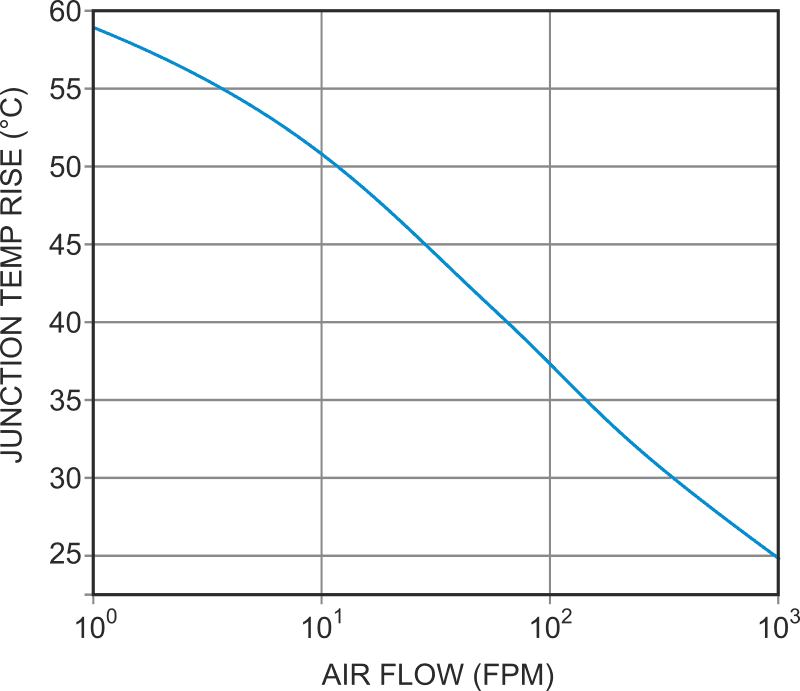
| Figure 1. | The TO-92 junction temperature delta versus air speed at 320 mW showing the nonlinear relationship between airflow and sensor temperature. |
The Figure 1 curve conforms to the empirical formula below, relating junction temperature to power dissipation and airspeed for a self-heated transistor in TO-92:
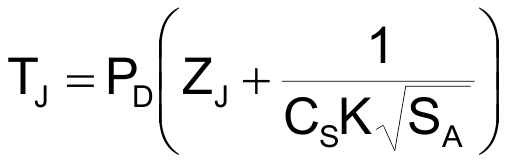
where:
TJ = junction temperature rise above ambient (°C)
PD = junction power dissipation (W)
ZJ = junction-to-case thermal impedance = 44 °C/W
CS = still-air case-to-ambient conductivity = 6.4 mW/°C
K = “King’s Law” thermal diffusion constant = 0.75 mW/°C/√fpm
SA = air speed in fpm
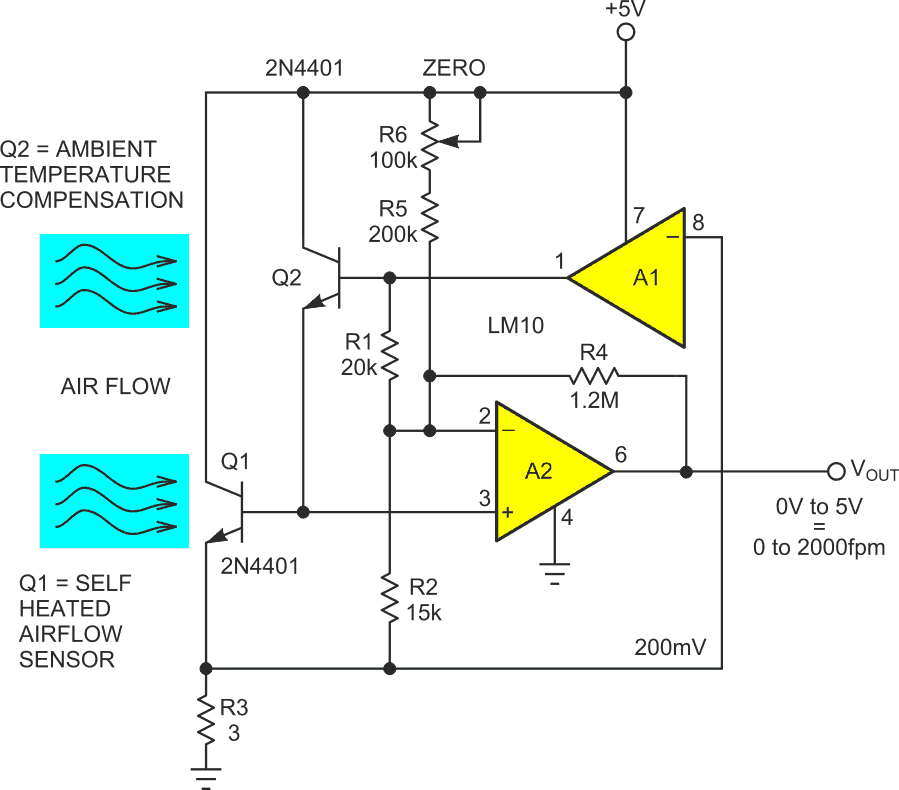
Figure 2 shows a practical thermal sensor circuit organized around a Darlington transistor pair: Q1 and Q2.
 |
|
| Figure 2. | The self-heated Darlington thermal airflow sensor. |
Q1 plays the role of self-heated sensor. Its VBE tempco converts temperature into voltage at –1.5 mV/°C. LM10 200 mV reference A1 regulates Q1 current to 0.2 V/R3 = 67 mA, thereby forcing Q1’s power dissipation to a constant 67 mA × 4.8 V = 320 mW. The resulting ambient versus junction temperature differential provides an airspeed readout as it cools from 64 °C at 0 fpm, to 22 °C at 2000 fpm, with a corresponding 63 mV rise in VBE from 654 mV at 0 fpm to 717 mV at 2000 fpm.
Meanwhile, Q2 provides airspeed-independent ambient temperature compensation.
Feedback through R4 and the accompanying resistor network set a 0-2000 fpm = 0-5 V scale factor with R6 providing zero-flow adjustment. But if meaningful conversion and acquisition of the flow signal are to happen, something will have to be done about that hideous nonlinearity.
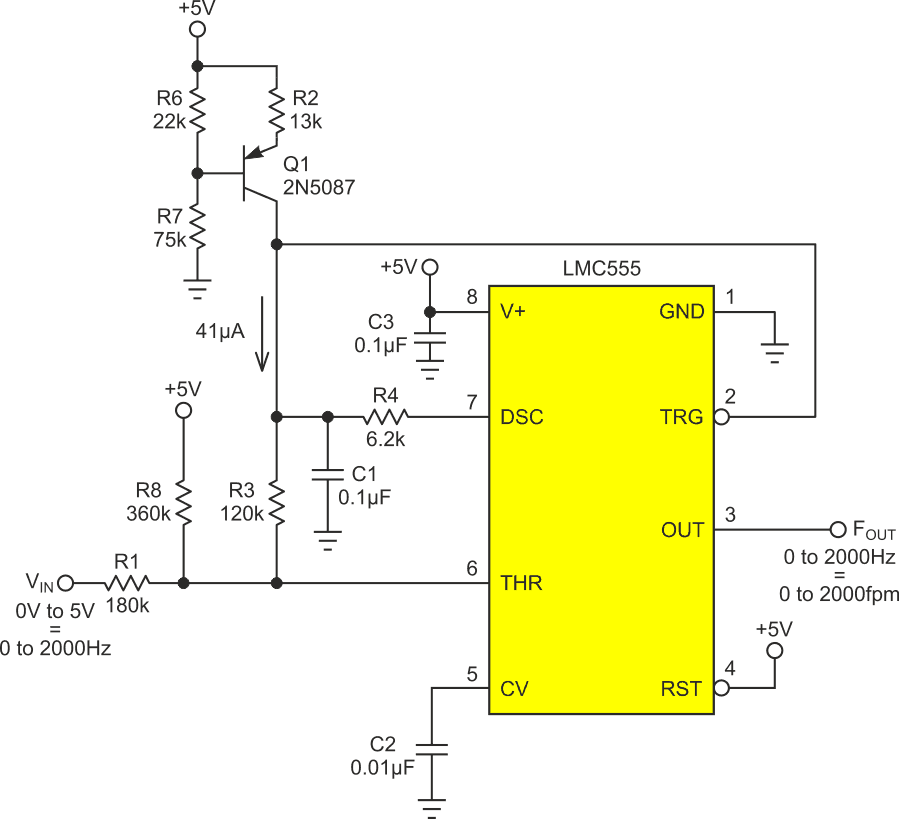
Figure 3 is that something.
 |
|
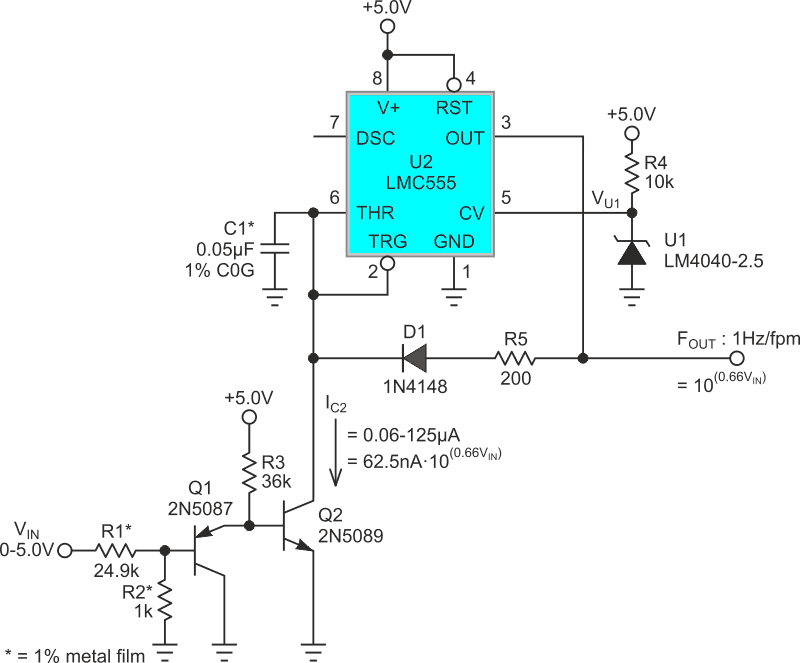
| Figure 3. | The nonlinear VFC is shown, with U1 configured in a 555 astable topology and a VIN resistor network, providing a solution for the previous nonlinearity. |
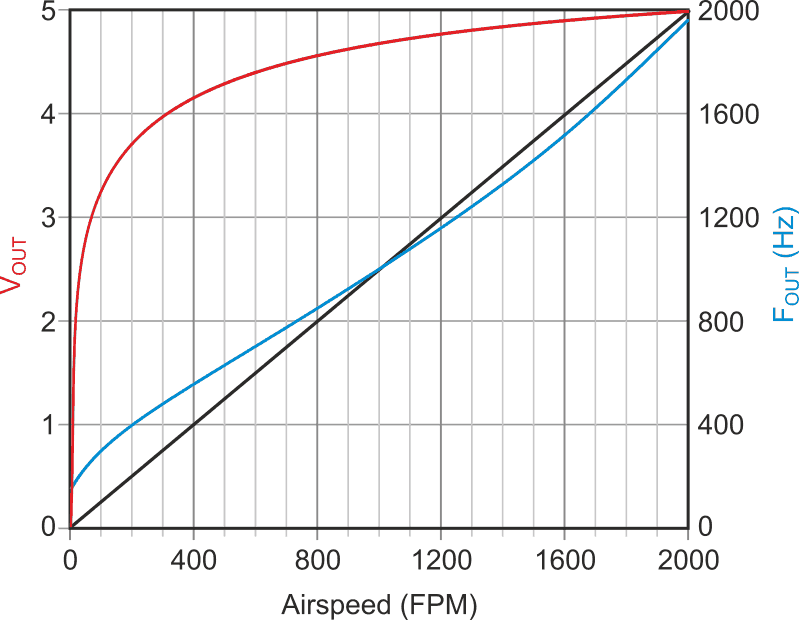
U1 is configured in a fairly typical 555 astable topology, except that the VIN resistor network acts to offset VTHR proportionately to VIN. Thus, as VIN moves from 0 to 5 V, corresponding to an airspeed excursion from 0 to 2000 fpm, the maxima of the VTHR timing ramp begin moving from just barely above the 2/3V+ threshold (corresponding to ~0 Hz), while the minima approach that limit (corresponding to ~2000 Hz). So, as VIN increases in response to increasing airspeed, the timing ramp at pin 6 has a steadily decreasing amplitude. This increases the rate of Hz versus fpm to cancel the opposite behavior of King’s Law (Figure 4’s red curve).
 |
|
| Figure 4. | The linearized VFC airflow response (blue) where the increasing rate of Hz versus fpm cancels the nonlinear effects of King’s Law to yield a 1 Hz = 1 fpm calibration. |
The resultant strongly nonlinear V to F conversion curve provides reasonable linearity compensation of Figure 2’s sensor strongly nonlinear response, as shown in Figure 4’s blue curve to yield a net 1 Hz = 1 fpm calibration.
Finally, Figure 3’s Q1 PNP current source probably needs a word of explanation. Its ~–2 mV/ °C VBE temperature dependence, in combination with the surrounding RS, causes its collector current to have an ~+0.3%/°C tempco, which would seem to be a bad thing for conversion accuracy. But it’s just the opposite, Q1’s tempco improves the accuracy of the air speed measurement by compensating for the variation of air density with temperature.
According to ol’ Jacques Clapeyron’s 1834 Ideal Gas Law (PV = nRT), air density (molecules per unit volume = n/V), and therefore heat capacity per unit volume, is inversely proportional to absolute temperature (n/V = P/R/T). Therefore, an accurate measurement of air speed, which is proportional to air volume, implies a direct relationship to absolute temperature, equaling about +0.3%/°C at “room” temperature. Rising ambient temperature causes Q1’s rising collector current to speed up U1’s oscillation frequency by just that factor.
So. Kudos to Q1.
ADDENDUM:
Konstantin Kim’s klever komment
Konstantin Kim (May 3, 2023): “Figure1 looks quite linear In semi-log scale: https://ibb.co/wBGt9pM”
 |
|
| Figure 5. | Konstantin Kim’s Kurve. |
Indeed, it does! Which suggested that a relatively simple anti-log circuit might be able to do an acceptable job of straightening out Figure 1’s badly bent airflow response curve and do it with much less arbitrary fiddling and fudging than Figure 3’s somewhat ad-hoc approach.
So, I straightaway started scribbling and anti-log rolling. Figure 6 shows the circuit that resulted.
 |
|
| Figure 6. | The anti-log nonlinear VFC. |
Q1 and Q2 comprise a complementary-Darlington topology in which equal-but-opposite forward biases (i.e., PNP base/emitter junctions oppose NPN base/emitter junctions) act to null the respective bias voltages and temperature dependencies of the two-transistor base-emitter junctions so that:
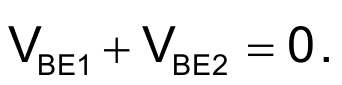
This allows us to take advantage of the anti-logarithmic relationship of Q2’s collector current versus VIN.
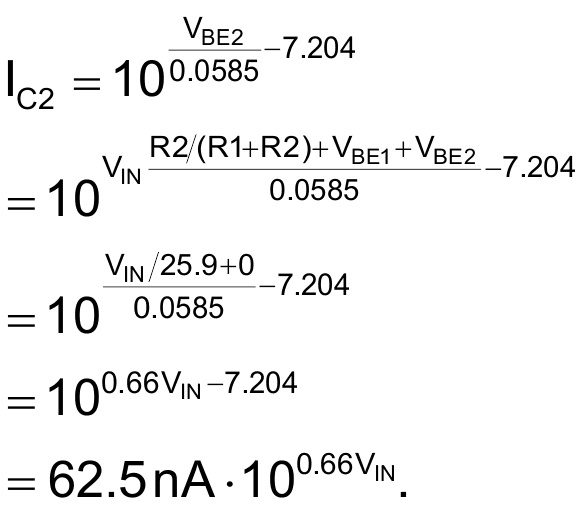
 |
|
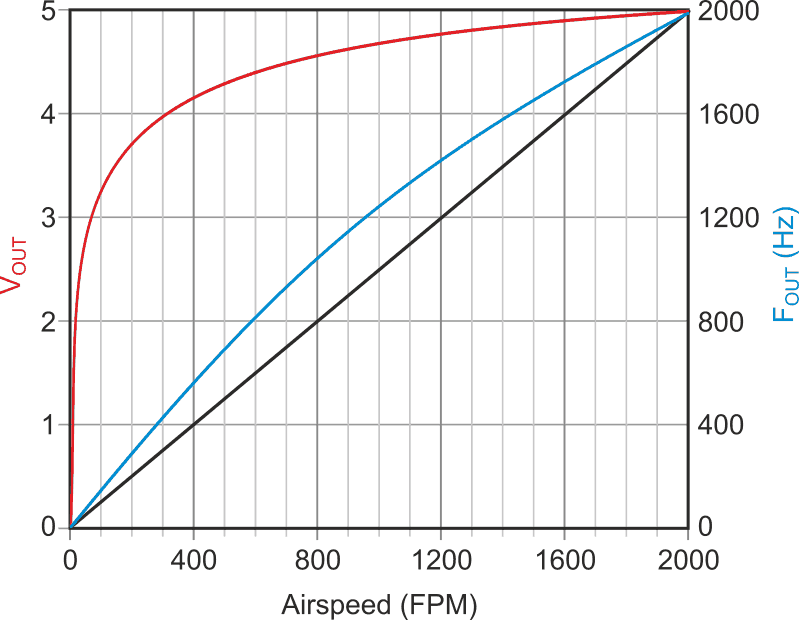
| Figure 7. | The anti-logarithmic linearization of Darlington airspeed sensor. |
Using the resulting current to discharge timing capacitor C1 generates a timing ramp fairly proportional to air speed and a VFC oscillation frequency of:
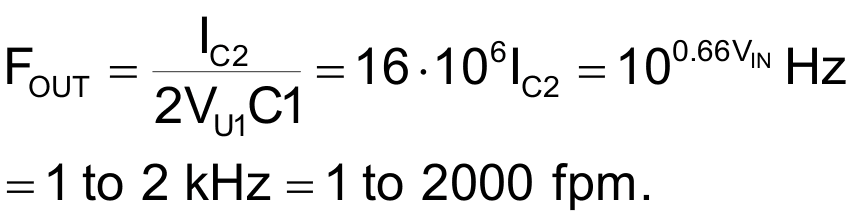
Figure 7 (blue curve) shows the result.
Kudos to Konstantin Kim!