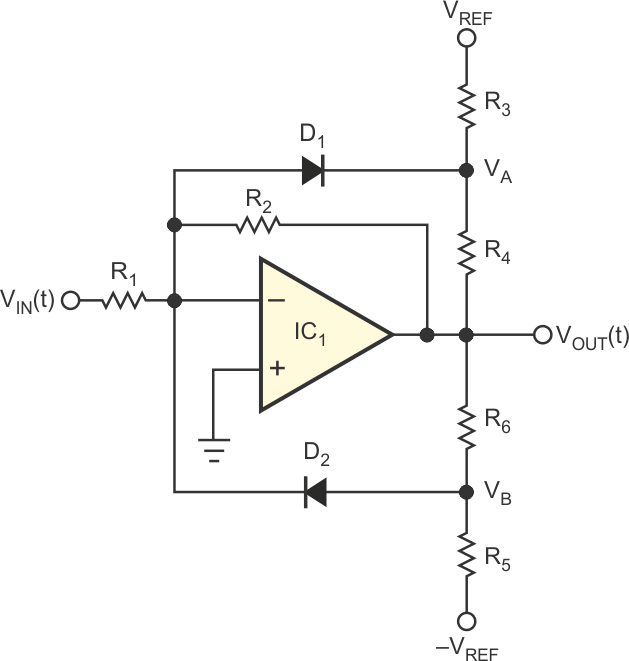
One of the most popular circuits for amplitude control in oscillators is the soft-limiter circuit (Figure 1a). When the output voltage, VOUT(t), is small, diodes D1 and D2 are off. Thus, all of the input current, VIN(t)/R1, flows through the feedback resistor, R2, and the output voltage is:
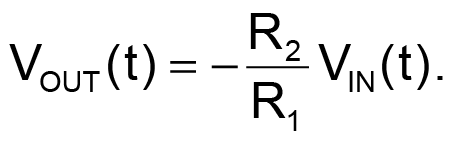
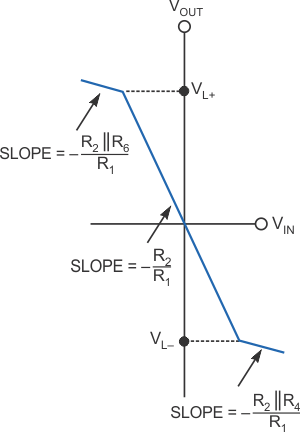
This portion is the linear part of the limiter-transfer characteristic in Figure 1b with slope of –(R2/R1).
|
||||||
| Figure 1. | Diodes in the feedback circuit form the basis of this soft limiter (a). The transfer characteristic of the limiter circuit shows inflection points when the diodes begin to conduct (b). |
|||||
On the other hand, when VOUT(t) goes positive, VA becomes more positive, thus keeping D1 off; however, VB becomes less negative. Then, if you continue to decrease VIN(t), you will reach a positive value of the output voltage, at which VB becomes approximately 0.7 V, and diode D2 conducts. Thus, the positive-limiting value at the output, VL+, is:
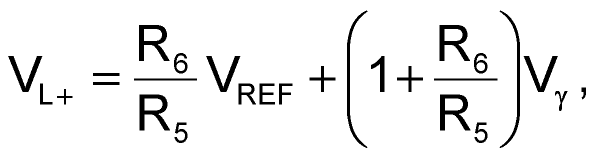
where Vγ is the forward voltage of the diodes – approximately 0.7 V. If VIN(t) decreases beyond this value, VOUT(t) will increase, more current is injected into diode D2, and VB remains at approximately –Vγ. Thus, the current through R5 remains constant, and the additional diode current flows through R6. Therefore, R6 appears, in effect, in parallel with feedback resistor R2, and the incremental gain, AV, ignoring the diode’s resistance, in the positive-limiting region is:
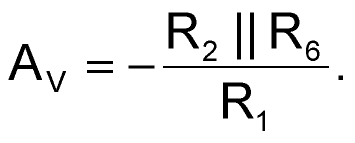
Note that, to make the slope of the transfer characteristic small in the limiting region, you should select a low value for R6. You can derive the transfer characteristic for positive VIN(t) or negative VOUT(t) in a manner identical to that of the above description. You can easily see that, for a positive VIN(t), diode D1 plays an identical role to the one that diode D2 plays for negative VIN(t). So, the negative-limiting level, VL–, is:
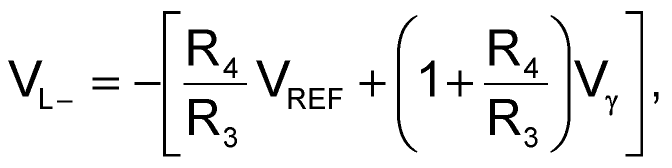
and the slope of the transfer characteristic in the negative-limiting region is:
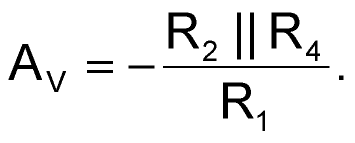
Note that increasing R2 results in a higher gain in the linear region and keeps VL+ and VL– unchanged. When you remove R2, the soft limiter turns into a comparator.
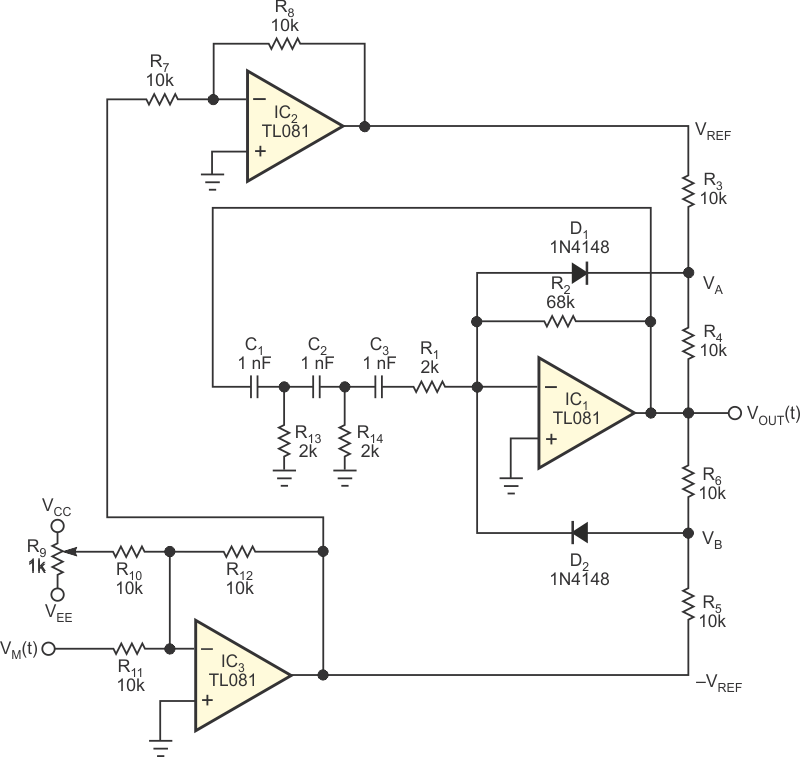
Thus, the circuit of Figure 1a functions as a soft limiter, and you can independently adjust the limiting levels VL+ and VL– by selecting the appropriate resistor values and reference voltages, ±VREF. Therefore, you can use a control voltage to change these limiting levels. You can base a simple AM modulator on this configuration. The RC (resistance/capacitance) phase-shift oscillator in Figure 2 includes a soft limiter in its voltage amplifier. You can alternatively use any similar RC or LC (inductance/capacitance) oscillator. You can modify the reference voltages, VREF and –VREF, with the input modulating voltage, VM(t). This voltage dynamically adjusts the saturation levels of the oscillator’s output. The ratio of the limiter resistors determines the output amplitude and the modulation index.
 |
||
| Figure 2. | Inserting the soft limiter into the feedback loop of a phase-shift oscillator enables a simple AM modulator. |
|
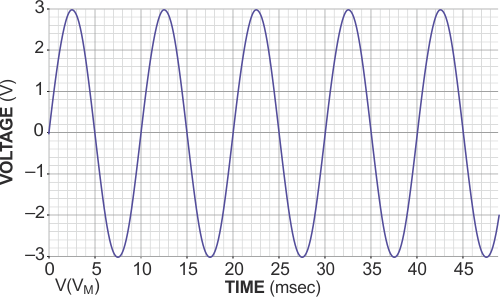
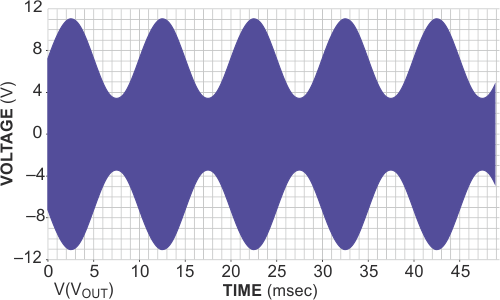
Figure 3 shows the waveforms of the modulating input, VM(t), and the oscillator’s modulated output, VOUT(t), with the component values of Figure 2. In this case, VM(t) is a sinusoidal waveform with an amplitude equal to 3 V, and trimmer R9 adds a 5 V offset voltage. The circuit works in a similar way to a four-quadrant analog multiplier.
|
||||||
| Figure 3. | The modulating input, VM(t) to the circuit in Figure 2 (a) obtains the modulated output voltage, VOUT(t) (b). |
|||||
Reference
- Sedra, Adel S, and Kenneth C Smith, Microelectronic Circuits: Fourth Edition, ISBN 0-19-511663-1, 1998, Oxford University Press, New York.