High school trigonometry combined with four-quadrant multipliers can be exploited to yield sinusoidal frequency doublers. Nothing non-linear is involved, which means no possibly strident filtering requirements.
Starting with some sinusoidal signal and needing to derive new sinusoidal signals at multiples of the original sinusoidal frequency, a little trigonometry and four-quadrant multipliers can be useful. Consider the following SPICE simulation in Figure 1.
 |
|
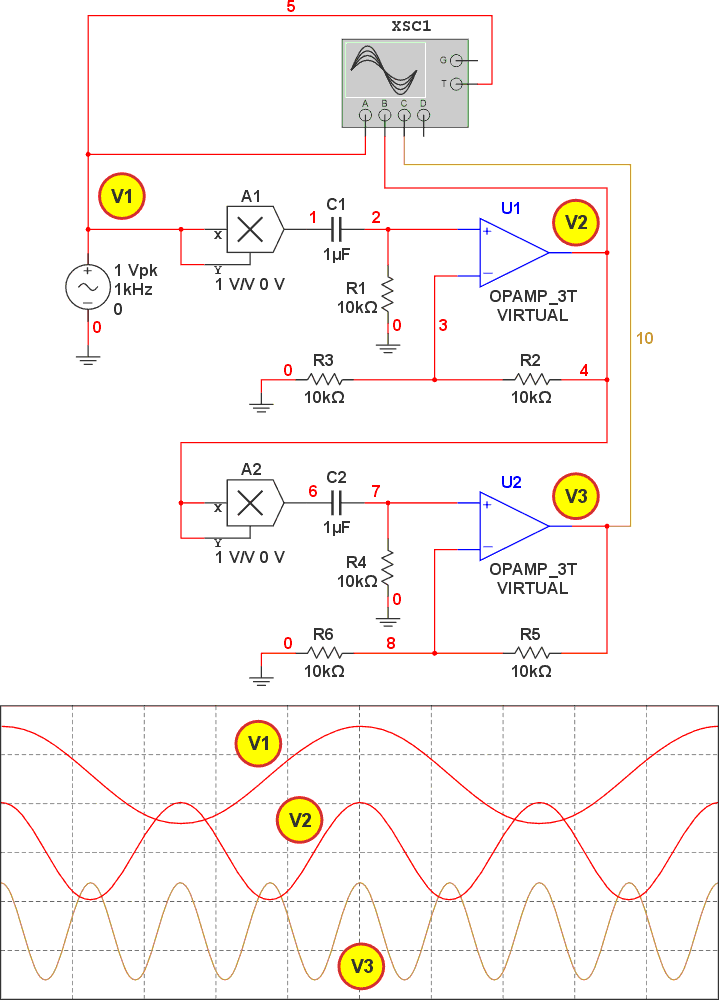
| Figure 1. | Two analog frequency doublers, A1 + U1 and A2 + U2, in cascade to form a frequency quadruple. |
The above sketch shows the pair A1 and U1 configured as a frequency doubler from V1 to V2, and the pair A2 and U2 configured as another frequency doubler from V2 to V3. Together, the two of them form a frequency quadrupler from V1 to V3. With more circuits, you can make an octupler and so on within the bandwidth limits of the active semiconductors, of course.
Frequency doubler operation is based on these trigonometric identities:
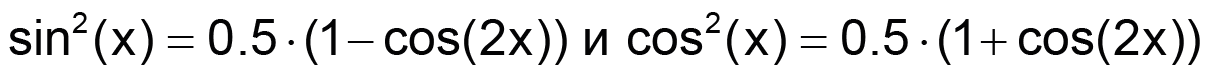
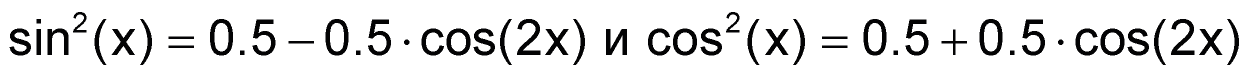
Take your pick, both equations yield a DC offset plus a sinusoid at twice the frequency you started with. Do a DC block as with C1 and R1 above, and you are left with a doubled-frequency sinusoid at half the original amplitude. Follow that up with a times two gain stage, and you have made a sinusoid at twice the original frequency and at the same amplitude with which you started.
This way of doing things takes less stuff than having to do some non-linear process on the input sinusoid to generate a harmonic comb and then having to filter out everything except the one frequency you want.
Although there might actually be some other harmonics at each op-amp output, depending on how non-ideal the multiplier and op-amp might be, this process does not nominally generate other unwanted harmonics. Such harmonics as might incidentally arise won’t require a high-performance filter for their removal.