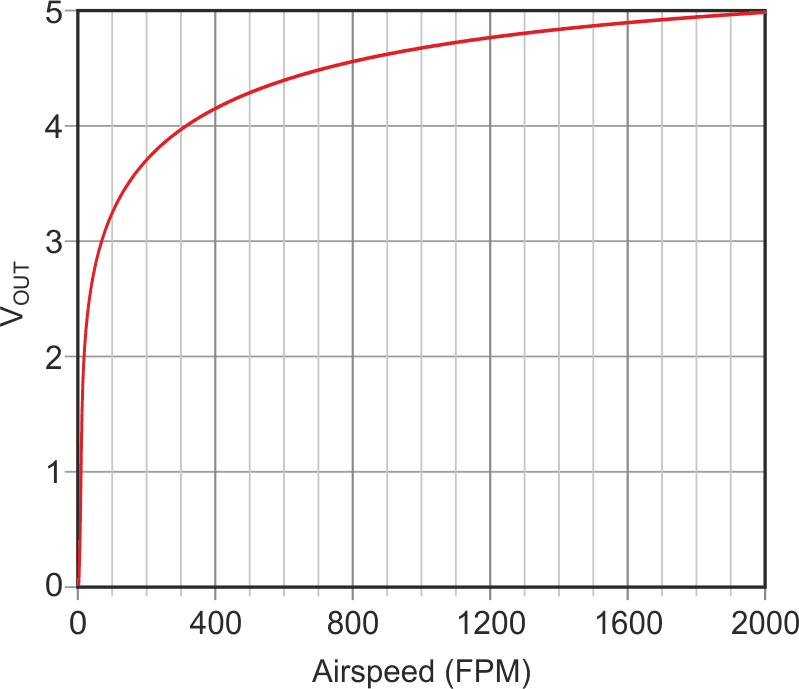
Awhile back I published a simple design idea for a thermal airspeed sensor based on a self-heated Darlington transistor pair (Ref, 1). The resulting sensor is simple, sensitive, and solid-state, but suffers from a radically nonlinear airspeed response, as shown in Figure 1.
 |
|
| Figure 1. | The VOUT versus airspeed response of the thermal sensor is very nonlinear. |
Veteran design idea contributor Jordan Dimitrov has provided an elegant computational numerical solution for the problem that makes the final result nearly perfectly linear. He details it in “Proper function linearizes a hot transistor anemometer with less than 0.2 % error“ (Ref. 2).
However, a consequence of performing linearization in the digital domain after analog to digital conversion is a significant increase in required ADC resolution, e.g., from 11 bits to 15, here’s why…
Acquisition of a linear 0 to 2000 fpm airspeed signal resolved to 1 fpm would require an ADC resolution of 1 in 2000 = 11 bits. But inspection of Figure 1’s curve reveals that, while the full scale span of the airspeed signal is 5 V, the signal change associated with an airspeed increment of 1999 fpm to 2000 fpm is only 0.2 mV. Thus, to keep the former on scale while resolving the latter, needs a minimum ADC resolution of:
1 in 5/0.0002 = 1 in 25,000 = 14.6 bits
15-bit (and higher resolution) ADCs are neither rare nor especially expensive, but they’re not usually integrated peripherals inside microcontrollers as mentioned in Mr. Dimitrov’s article. So, it seems plausible that a significant cost might be associated with provision of an ADC with resolution adequate for his design. I wondered about what alternatives might exist.
Here’s a design for simple and cheap high-resolution ADC built around an old, inexpensive, and widely available friend: the 555 analog timer chip.
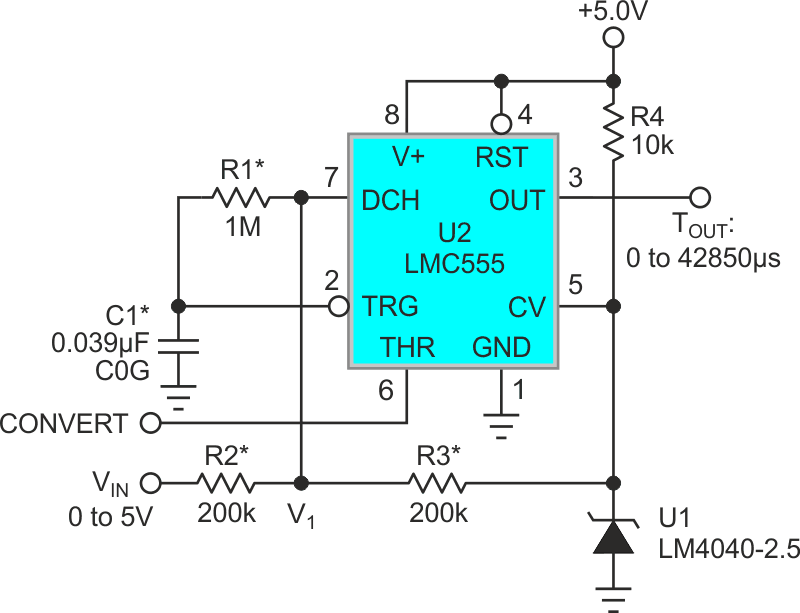
See Figure 2 for the schematic.
 |
|
| Figure 2. | High resolution voltage-to-time ADC suitable for self-heated transistor anemometer linearization. An asterisk denotes precision components (1% tolerance). |
Signal acquisition begins with the R2, R3, U1 summation network combining the 0 to 5 V input signal with U1’s 2.5 V precision reference to form:
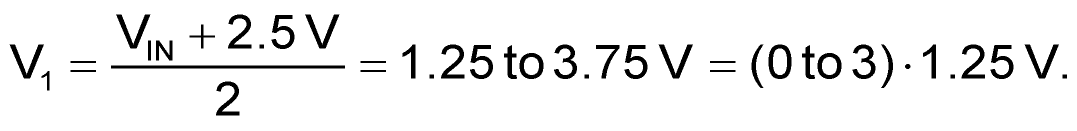
V1 accumulates on C1 between conversion cycles with a time constant of:
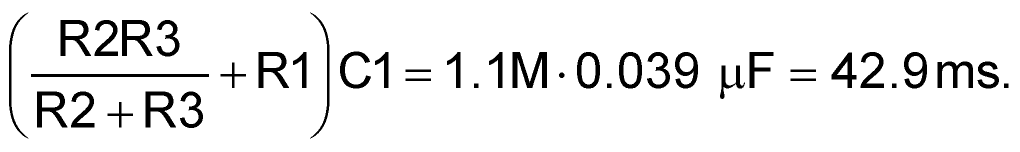
Thus, for 16 bit accuracy, a minimum settling time is required of:
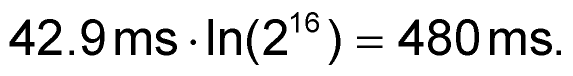
The actual conversion cycle can then be started by inputting a CONVERT command pulse (>2.5 V amplitude and >1 microsecond duration) to the 555 THR (threshold) pin 6 as illustrated in Figure 3.
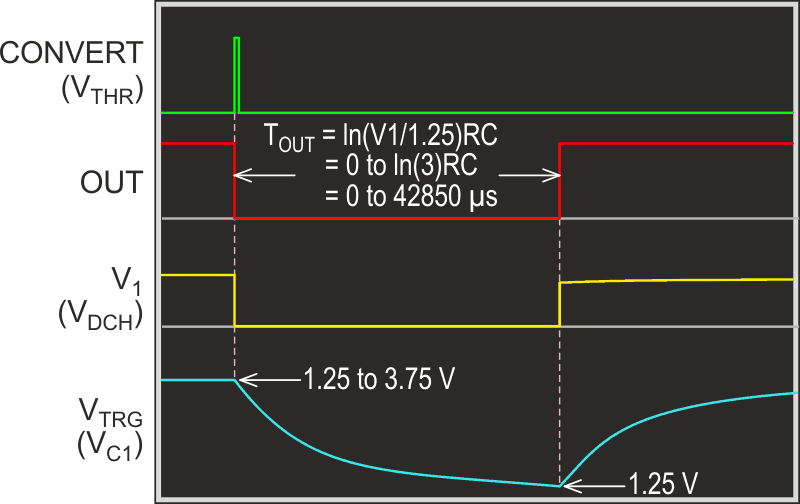 |
|
| Figure 3. | ADC cycle begins with a CONVERT THR pulse that generates an OUT pulse of duration TOUT = ln(V1/1.25 V)R1C1. |
The OUT pulse (low true) begins with the rising edge of CONVERT and is coincident with the 555 DCH (discharge) pin 7 being driven to zero volts, beginning the discharge of C1 from V1 to the 555 trigger voltage (VTRG = VC/2 = 1.25 V) on pin 7. The duration of C1 discharge and TOUT, accumulated digitally (a counter of 16 bits and resolution of 1 µs is adequate) by a suitable microcontroller, are given by:
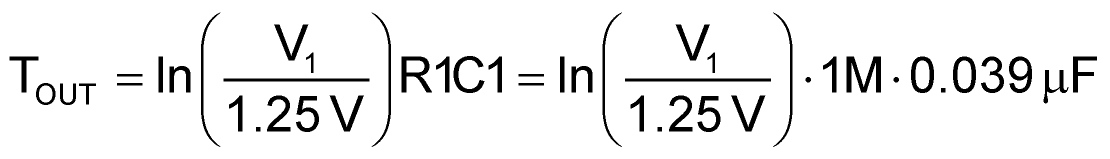
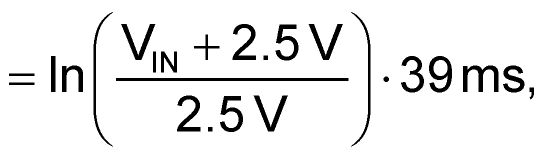
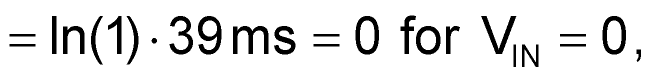
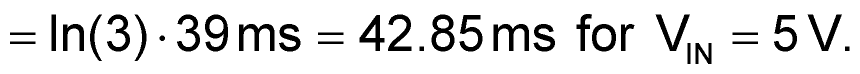
At the end of TOUT, DCH is released so the recharge of C1 can commence, and the conversion result:
N = 1 MHz · TOUT
is available for linearization computation. The math to decode and recover VIN is given by:
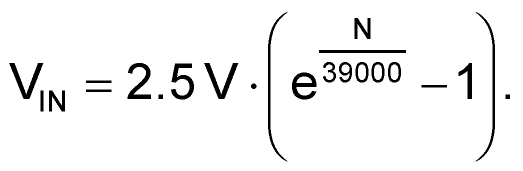
A final word. You may be wondering about something. Earlier I said a resolution of 1 part in 25000 = 14.6 bits would be needed to quantify the VIN delta between 1999 and 2000 fpm. So, what’s all this 42850 = 15.4 bits stuff?
The 42850 thing arises from the fact that the instantaneous slope (rate of change = dV/dT) of the C1 discharge curve is proportional to the voltage across, and therefore the current through, R1. For a full-scale input of VIN = 5 V, this parameter changes by a factor of 3 from V1 = 3.75 V and 3.75 µA at the beginning of the conversion cycle to only 1.25 V and 1.25 µA at the end. This increase in dV/dT causes a proportional but opposite change in resolution. Consequently, to achieve the desired 25000:1 resolution at VIN = 5 V, a higher average resolution is needed.
The necessary resolution factor bump is square root (3) = 1.732… of which 42850/25000 = 1.714 is a rough and ready, but adequate, approximation.
References
- Woodward, Stephen. ”Nonlinearities of Darlington airflow sensor and VFC compensate each other.”
- Dimitrov, Jordan. ”Proper function linearizes a hot transistor anemometer with less than 0.2 % error.”