Digital potentiometers (digiPOTs) are versatile and can be used in a wide variety of applications, for example, for filtering or generating ac signals. However, sometimes the frequency must be able to be varied and adapted to the desired application. Programmable solutions enabling the frequency to be adjusted via an appropriate interface are extremely helpful in such designs and, in some cases, can greatly facilitate development. A method of relatively easily constructing a programmable oscillator in which the oscillation frequency and amplitude can be adjusted independently of each other by using digiPOTs is described in this article.
 |
|
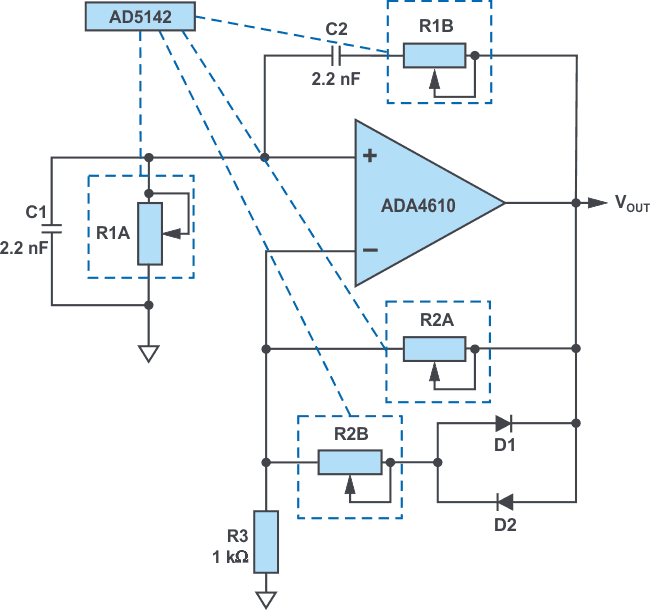
| Figure 1. | Programmable Wien-bridge oscillator with amplitude stabilization wherein the resistors are replaced by digiPOTs. |
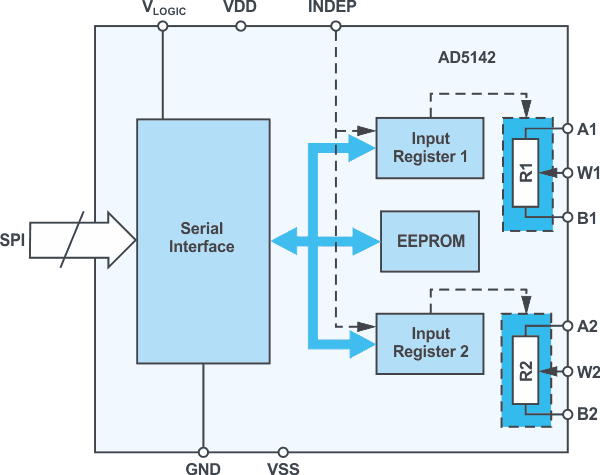
Figure 1 shows a typical diode-stabilized Wien-bridge oscillator with which precise sinusoidal signals in the range of approximately 10 kHz to 200 kHz can be realized at the output (VOUT). Wien-bridge oscillators are characterized by the fact that one bridge path is formed by a band-pass filter and the other by a voltage divider. This example uses – in addition to the ADA4610-1 rail-to-rail precision amplifier – the AD5142 digiPOT, which contains two independently controllable potentiometers, each with a resolution of 256 steps. The programming of the resistance values is done via an SPI, as shown in Figure 2. Alternatively, the AD5142A, which can be controlled via an I2C, can be used. Both variants are available as 10 kΩ or 100 kΩ potentiometers.
 |
|
| Figure 2. | Block diagram of the AD5142. |
In the classic oscillator circuit shown in Figure 1, the path with R1A, R1B, C1, and C2 forms the positive feedback, whereas negative feedback is provided via R2A, R2B, and the two parallel diodes D1 and D2, or their resistance RDIODE. Here, Equation 1 applies:
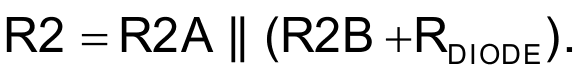 |
(1) |
To achieve sustained stable oscillation, it is necessary to eliminate the phase shift of the loop gain. Expressed by formulas, the following term is yielded for the oscillator frequency:
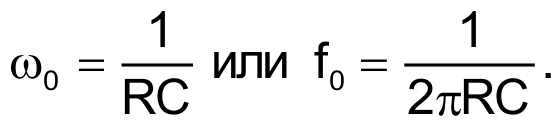 |
(2) |
Here, R is the programmable resistance value on the AD5142:
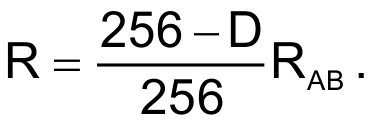 |
(3) |
D is the decimal equivalent of the digital code programmed in the AD5142, and RAB is the total resistance of the potentiometer.
To sustain oscillation, the Wien-bridge should be relatively balanced – that is, the gain of the positive feedback and the gain of the negative feedback must be coordinated. If the positive feedback (gain) is too large, the oscillation amplitude or VOUT will increase until the amplifier saturates. If the negative feedback dominates, then the amplitude will accordingly be damped out.
For the circuit shown here, the gain R2/R1 should be set to approximately 2 or somewhat higher. This ensures that the signal starts oscillating.
However, the alternate turn-on of the diodes in the negative feedback loop also causes the gain to be temporarily less than 2 and thereby stabilizes the oscillation.
Once the desired oscillation frequency is determined, the amplitude of oscillation can be tuned independently of the frequency via R2. This can be calculated as follows:
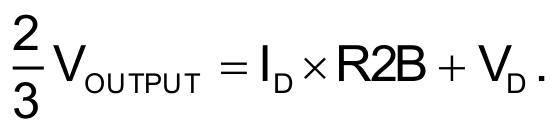 |
(4) |
The variables ID and VD thereby, respectively, represent the diode forward current and diode forward voltage across D1 and D2. If R2B is shorted, an oscillation amplitude of approximately ±0.6 V is yielded. With the correct order of magnitude for R2B, equilibrium can be achieved so that VOUT converges. In the circuit shown in Figure 1, a separate 100 kΩ digiPOT is used for R2B.
Conclusion
With the described circuit and a 10 kΩ dual digiPOT, oscillation frequencies of 8.8 kHz, 17.6 kHz, and 102 kHz can be tuned with resistance values of 8 kΩ, 4 kΩ, and 670 Ω, respectively, with a low frequency error of just ±3%. Higher output frequencies are also possible with an effect on the frequency error. For example, at 200 kHz, the frequency error will increase to 6%.
When using such circuits in frequency-dependent applications, it is also important not to violate the bandwidth limit of a digiPOT as it is a function of the programmed resistance. In addition, the frequency tuning in Figure 1 requires that the resistance values for R1A and R1B be the same. However, the two channels can only be set successively and lead to a momentary critical intermediate state. This might be unacceptable for certain applications. In such cases, it is possible to use digiPOTs with daisy-chain mode (for example, AD5204) to allow both resistance values changing at the same time.