Perhaps the most elementary rule of control-loop design theory is that feedback-loop performance is fundamentally linked to the careful choice – and stability – of loop gain. Insufficient loop gain leads to poor setpoint accuracy. Too much gain can induce feedback instabilities, such as overshoot, ringing, and, ultimately, oscillation. Therefore, the greater the accuracy you expect from a control system, the more critical maintaining near-optimal loop gain becomes. Precision temperature-control loops are no exception.
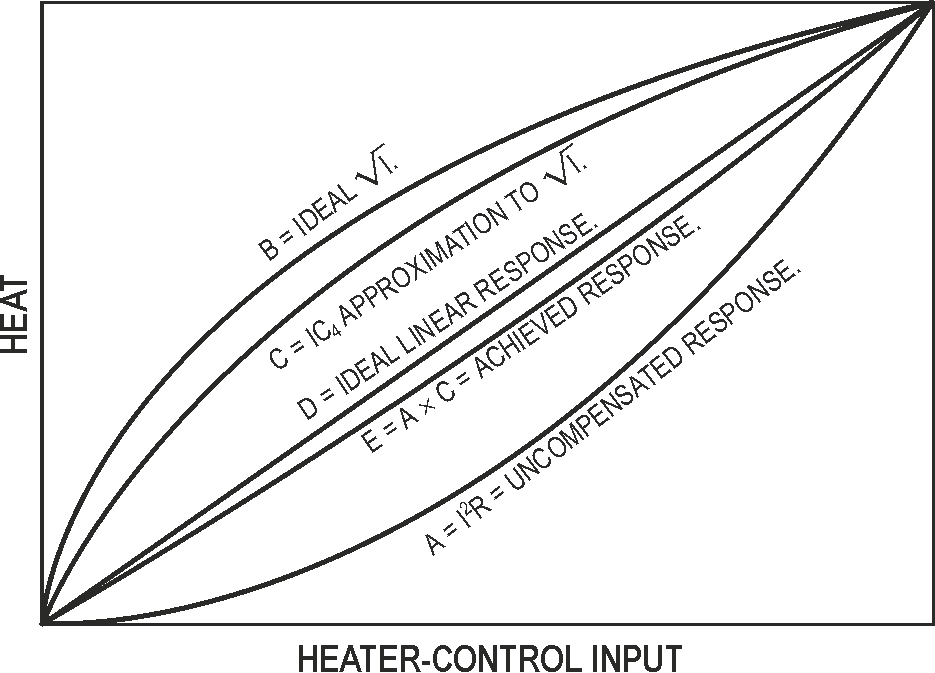
Given the aforementioned truisms, it's surprising that the following rule of designing high-precision thermostats receives so little notice: The thermal output (which is power, the primary feedback parameter) from a resistive heater is proportional to the current squared. In Figure 1, Curve A illustrates this elementary relationship.
 |
||
| Figure 1. | Multiplying the uncompensated square-law response (A) by the square-root current response (C) from IC4 yields a linear response of heat versus heater-control output. |
|
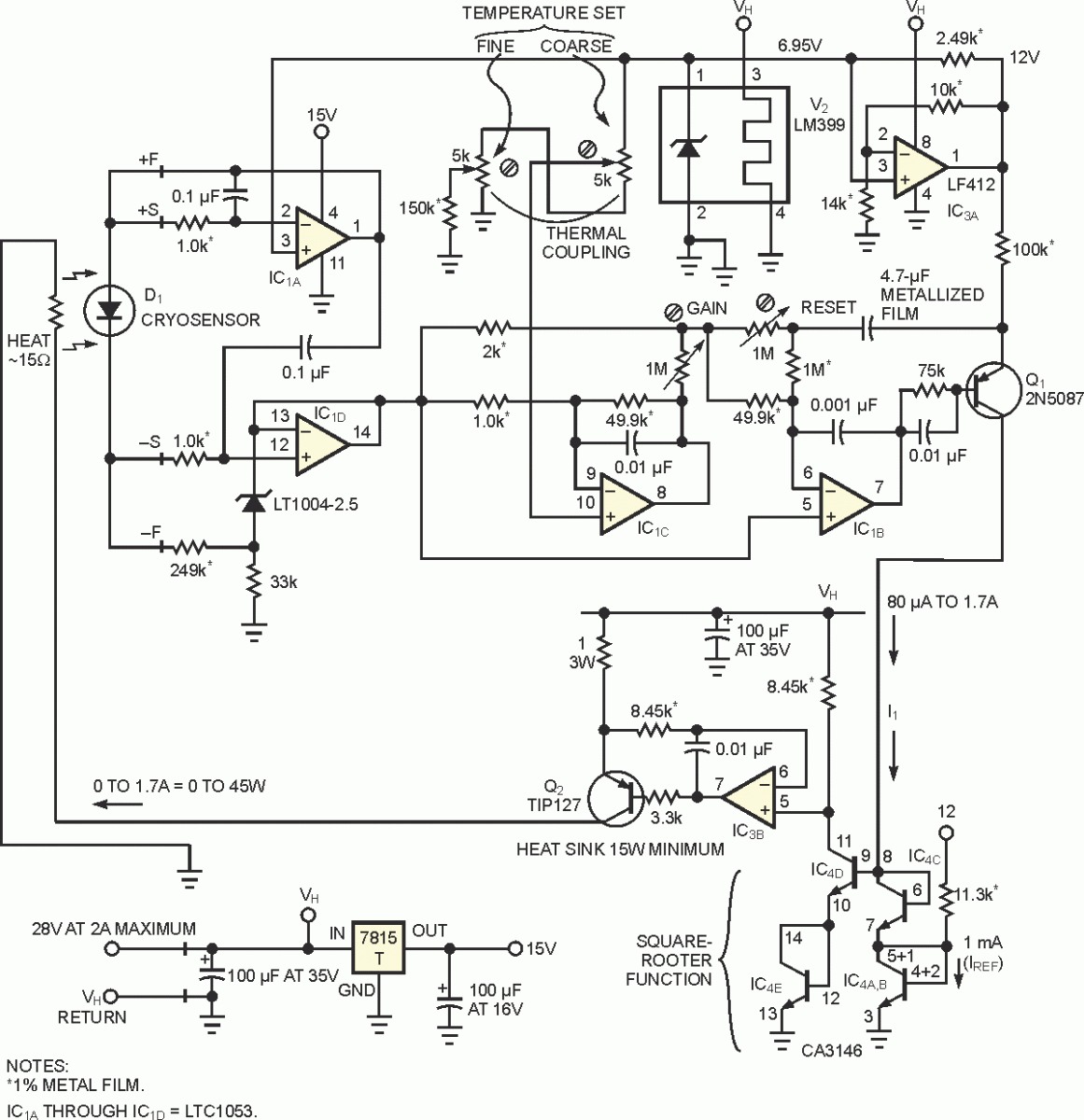
Therefore, the overall thermostat loop gain is not constant but is instead proportional to heater input current. It consequently varies wildly in response to changes in ambient temperature and other factors that impact heat demand. The result is that it becomes more difficult to choose suitable loop parameters. The circuit in Figure 2 remedies these difficulties by inserting an analog square-root circuit ahead of the heater-drive circuit.
 |
||
| Figure 2. | The logarithmic response of transistors IC4A through IC4C results in a square-root function for the heater-control voltage. |
|
The circuit stabilizes the temperature of liquid-nitrogen-cooled solid-state infrared lasers in an airborne spectrometer. The cryosensor diode, D1 (2 mV/K), senses laser temperature and drives the PI (proportional-integral) control circuit comprising error amplifier IC1C and error integrator IC1B. Q1 converts the resulting feedback correction voltage to a current-mode signal and applies the signal to the LM3146 transistor array, IC4. The array generates the square-root function. Analog aficionados will be quick to point out that using IC4 is not the most accurate way to approximate a square-root curve. However, this method is adequate for making the feedback linear and stabilizing the loop gain. In operation, array transistors IC4A through IC4C combine the current, I1, from Q1 with the reference current (IREF) to produce a logarithmic control voltage proportional to
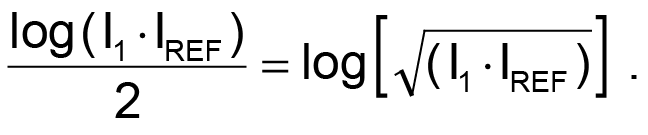
The inherent matching of transistor parameters in the IC4 monolithic array results in an IC4E collector current of approximately
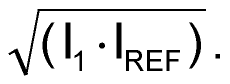
The IC3B-Q2 heater-driver circuit subsequently amplifies IC4E's output current by a factor of 8450 and applies the amplified current to the laser-cryostat heater.
Figure 1 shows five relevant curves. A is the uncompensated I2R heater transfer function. B is the ideal square-root function. C is the square-root approximation from the IC4 array, which you calculate assuming transistor betas of approximately 100. D is the product of A and B and represents the ideal compensated (linear) loop-gain linearization with constant loop gain. E is the product of A and C and is the achieved loop-gain linearization. The net result is a linear relationship between the control circuit and heater outputs and a consequent optimization of the cryostat's steady-state and dynamic stabilities over a range of ambient-heat loading. Without IC4, a gain setting adequate for setpoint stability at low heater powers is likely to be excessive and produce overshoot or oscillation at high heater powers.