A design idea with a 555 analog timer that can generate an arbitrary triangle/sawtooth with its waveshape and frequency controlled by pots.
If you could assemble the list of all the oscillators that have been designed around the 555 analog timer, it would boggle the mind. Variable duty cycle, linear ramp, triangle, sawtooth, etc. populate this crowded circuitry cornucopia. The topology described here explores some new and useful possibilities and so (hopefully) doesn’t simply add to the crush.
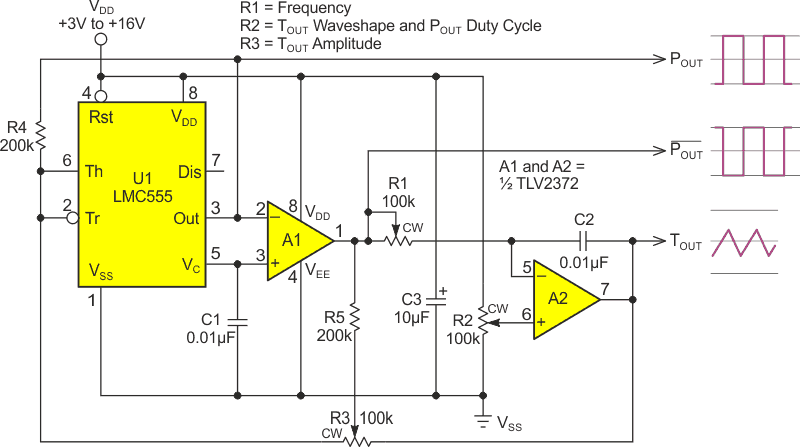
Figure 1 shows the new oscillator, based on CMOS 555 U1 in a feedback loop with RRIO (Rail-to-Rail Input-Output) op-amp integrator A2 generating a linear triangle output signal (TOUT) with adjustable frequency (via R1), waveshape (via R2), and amplitude (via R3). Here’s how it works.
 |
|
| Figure 1. | The triangle/sawtooth/etc. oscillator. |
A2’s integrator is inherently inverting, so a complementary signal inversion is necessary somewhere in the signal chain to undo the reversal and allow A2 to make positive feedback for U1. This is A1’s job – though duty as an elementary inverter is probably a bit demeaning for a self-respecting op-amp.
The differential between A1’s rail-to-rail output (–POUT = VSS to VDD) and waveshape-setting VR2 (likewise VSS to VDD) is the input integrated by A2, producing a linear ramp slope
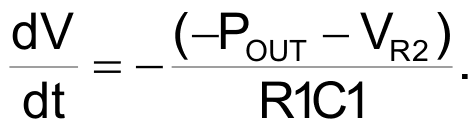
This relation makes oscillator frequency inversely proportional to R1, theoretically increasing without limit as R1 approaches full CW = zero resistance.
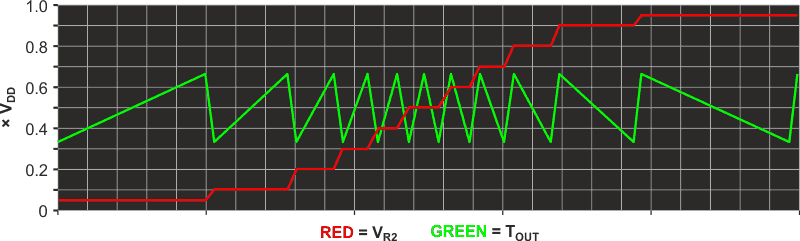
The (–POUT – VR2) differential relation makes the TOUT waveshape adjustable via R2. The effect on TOUT of twiddling R2 (from 0.05 to 0.95 CW) is shown in Figure 2. A2’s RR input makes this work even if R2 is run arbitrarily close to either VDD (fully CW) or VSS (fully CCW).
Per Figure 2, setting R2 to mid-span (0.5) yields a symmetrical triangle waveshape, while settings nearer 0 or 1.0 produce sawteeth. The duty cycle of pulse output POUT also follows R2, ranging from near 0% for R2 near zero, 50% for R2 at mid span, and approaching 100% for R2 near full CW, while inverse function –POUT provides the complement.
 |
|
| Figure 2. | The triangle output (TOUT) waveshape versus R2. |
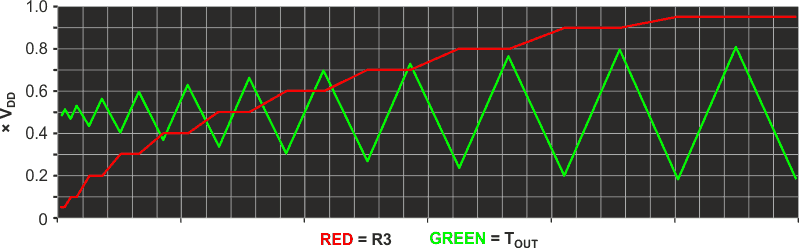
Figure 3 shows how TOUT amplitude is controlled by the R3, R4, R5 feedback loop, variable from near zero (R3 fully CCW) to 2VDD/3 (full CW) the latter being twice the usual 555 VDD/3 oscillation span. This works by summing adjustable ratios of the POUT and –POUT pulses with A2’s ramp before the composite signal is input to the Th (threshold) and Tr (trigger) pins of U1. This summation offsets the switching points of A2’s ramp. TOUT remains symmetrically centered around VDD/2.
 |
|
| Figure 3. | TOUT amplitude versus R3, 0 = Fully CCW, 1 = CW. |
Note that R3 has no effect on POUT or –POUT amplitudes, which always have full VSS to VDD excursions.
Oscillation frequency is affected by waveshape and amplitude changes, but waveshape and amplitude are independent of frequency and each other. Therefore the easiest setting method is to adjust waveshape (R2) and amplitude (R3) first, then set frequency (R1). This will minimize the need for repetitive interacting “tail-chasing” adjustments.
The 0.01 µF shown for C2 is appropriate for operating frequencies in the kHz range, but of course can be changed for almost any preferred range, increasing C2 for lower frequencies and decreasing it for higher.
All outputs are actively buffered and low impedance, making them insensitive to loading, and will seldom require additional buffering.
Temperature stability mostly depends on resistor and capacitor tempcos, because the 555 and 2372 are excellent in that department.
Total VDD current draw will depend on VDD, operating frequency, and output loading, but is typically less than 3 mA. This oscillator’s ability to work with supply voltages down to 3 V is lower than most other 555-based linear ramp generators.