A classic nonlinear analog function is the squaring circuit. It’s useful in power sensing, frequency multiplication, RMS computation, and many other odd jobs around the lab bench.
 |
|
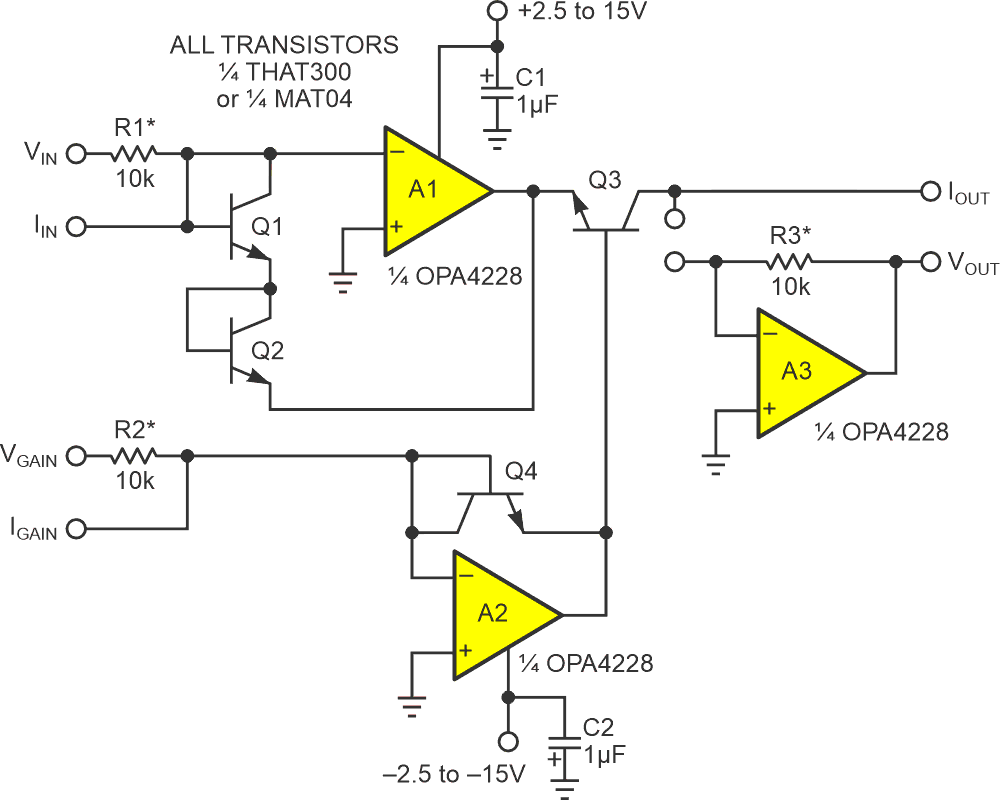
| Figure 1. | The squaring amplifier that is fast, temperature-compensated, calibration-free, and accurate (if the transistors are well matched). |
The version in Figure 1 is straightforward, fast, temperature-compensated, calibration-free, and if the transistors are well matched, accurate. The final output is as follows:

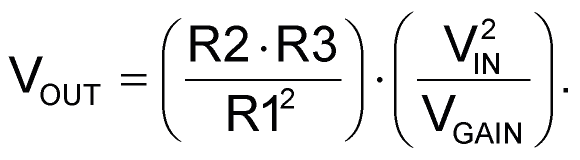
Its input can accept either voltage or current. It gains a bit of extra versatility from a separate gain factor control input, which can also accept voltage or current. Another boost in versatility comes from a similarly flexible output with both voltage and (inverted) current output mode. If the current mode is chosen, A3 and R3 can be omitted and a dual op-amp (OPA2228) used instead of the quad (OPA4228) illustrated.
The series connection of Q1 and Q2 generates a signal proportional to
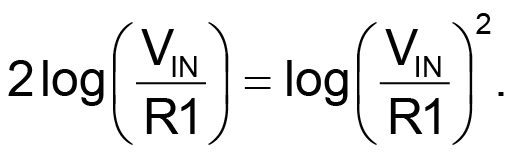
This is applied to antilogger Q3 ,which subtracts
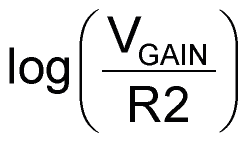
from it to generate a current of:
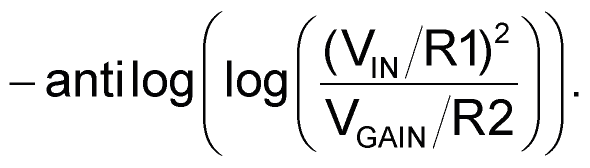
This is inverted and scaled by R3 and A3 to yield the final:
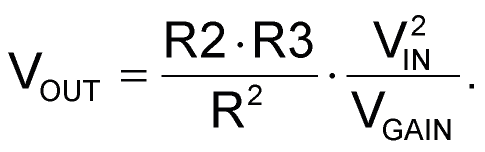
Note that if the three resistors are equal and VIN = VGAIN, then:
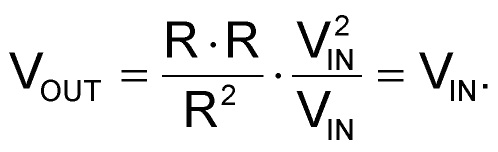
And, the squarer circuit will have unity gain.
Which is kind of a “square deal,” although I doubt it’s what Teddy Roosevelt had in mind when he made that phrase his 1904 campaign slogan.
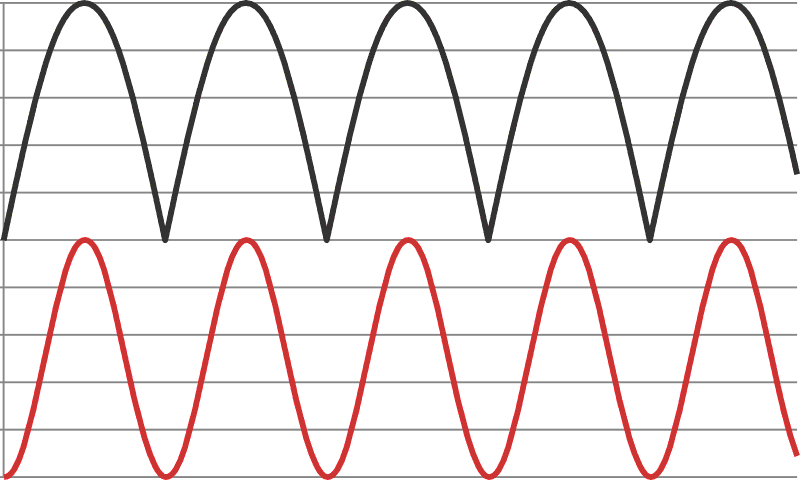
An interesting application happens when the squarer is combined with a full-wave precision rectifier (like the one in “New full-wave precision rectifier has versatile current mode output” (Ref. 1)). See Figure 2.
 |
|
| Figure 2. | The cascading full-wave rectifier (black) with squarer makes low distortion frequency doubler (red). |
Reference
- Woodward, Stephen. "New full-wave precision rectifier has versatile current mode output."