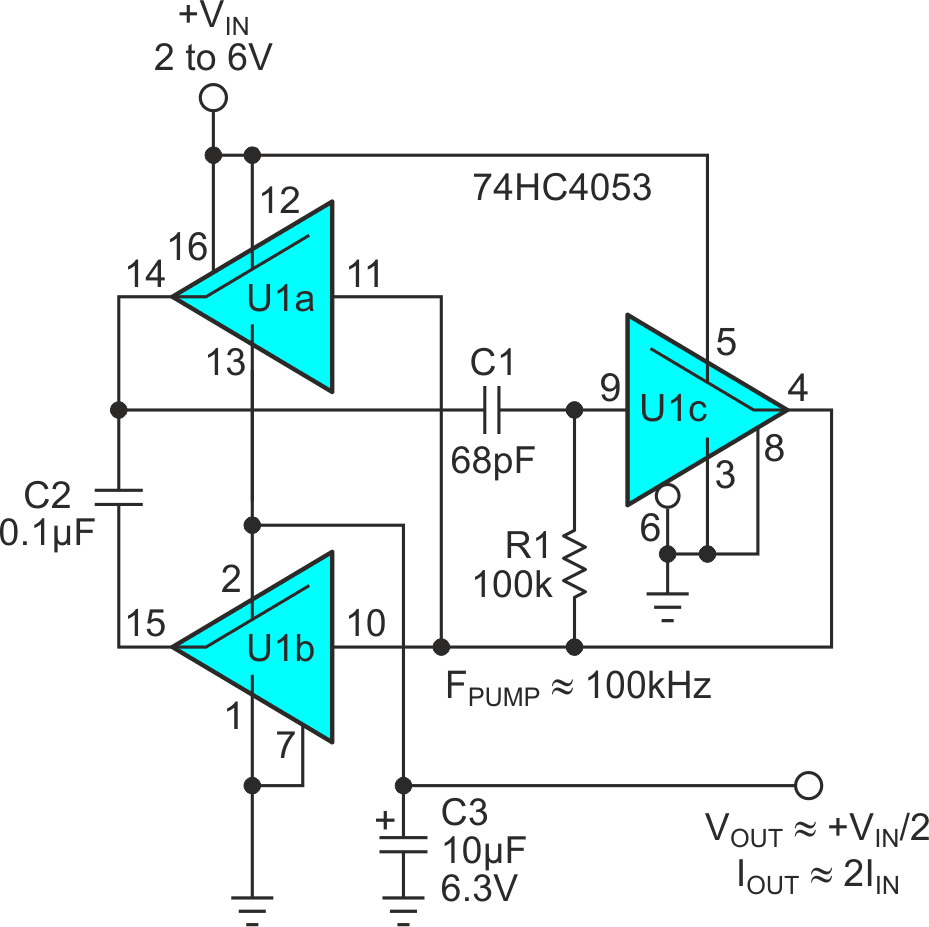
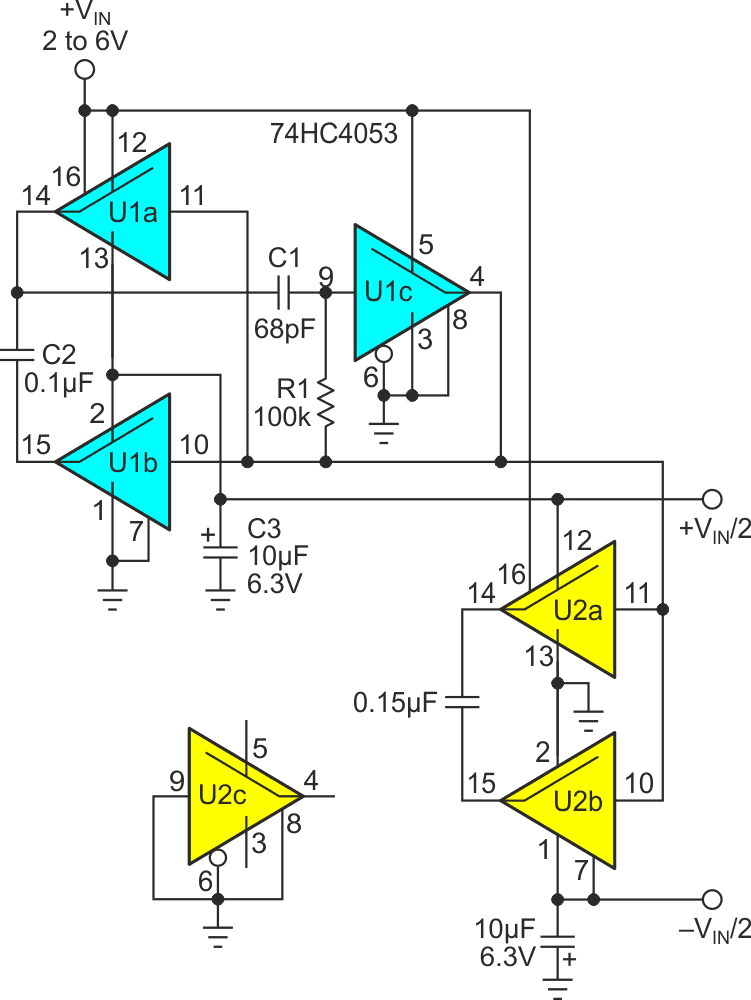
Capacitor type charge pumps are a well-known, simple, efficient, cost-effective (and therefore popular!) method for inverting and multiplying voltage supply rails. Perhaps less well known, however, is that they also work just as well for dividing voltage (while multiplying current). Figure 1 illustrates a VOUT = VIN/2, IOUT = IIN·2 example pump built around the venerable xx4053 CMOS triple SPDT switch.
 |
|
| Figure 1. | xx4053 based, 100 kHz, voltage-halving, current-doubling charge pump. |
Here’s how it works.
The R1C1 time constant couples the VIN/ppv square wave found at U1pin14 to U1pin9, creating an FPUMP oscillator frequency of (approximately):
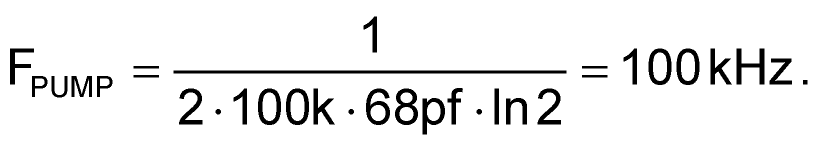
During the FPUMP negative half-cycle (U1pin4 = 0), the upper (U1pin14) end of C2 is connected to VIN while the lower end (U1pin15) end is connected to VOUT, thus charging C2 to:
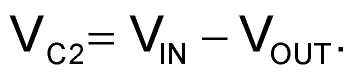
Then, during the following FPUMP positive half-cycle (U1pin4 = VIN), the upper end of C2 connects to VIN while the lower end connects to VOUT, and:
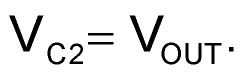
This deposits a quantity of charge onto C3 of:
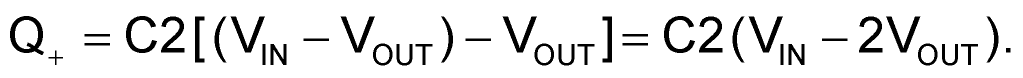
During the subsequent negative half-cycle, again:
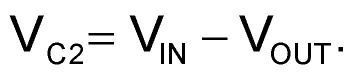
Depositing another charge onto C3 of:
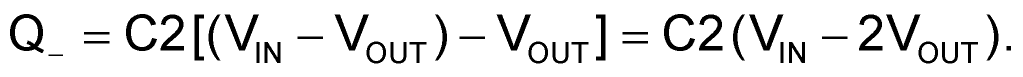
Thus, each full cycle of FPUMP deposits a net charge onto C3 of:
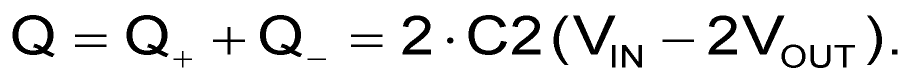
Which, if IOUT = 0, forces Q = 0 and therefore:
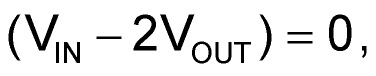
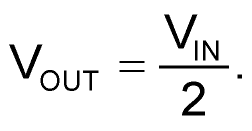
However, for the (much more interesting) case of IOUT > 0:
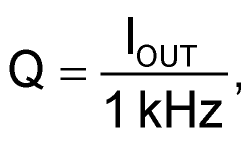
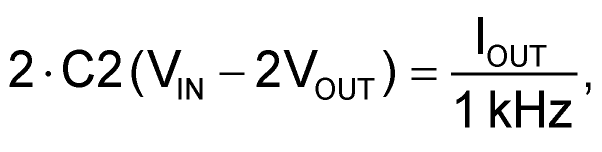
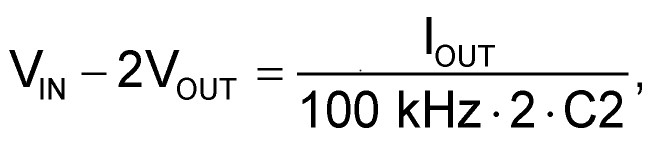
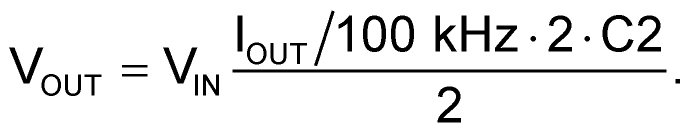
In other words, VOUT droops a bit as the output is loaded. This is because, for a finite C2 Q is also finite, but also to the fact that the U1a and U1b internal switches have non-zero ON resistances.
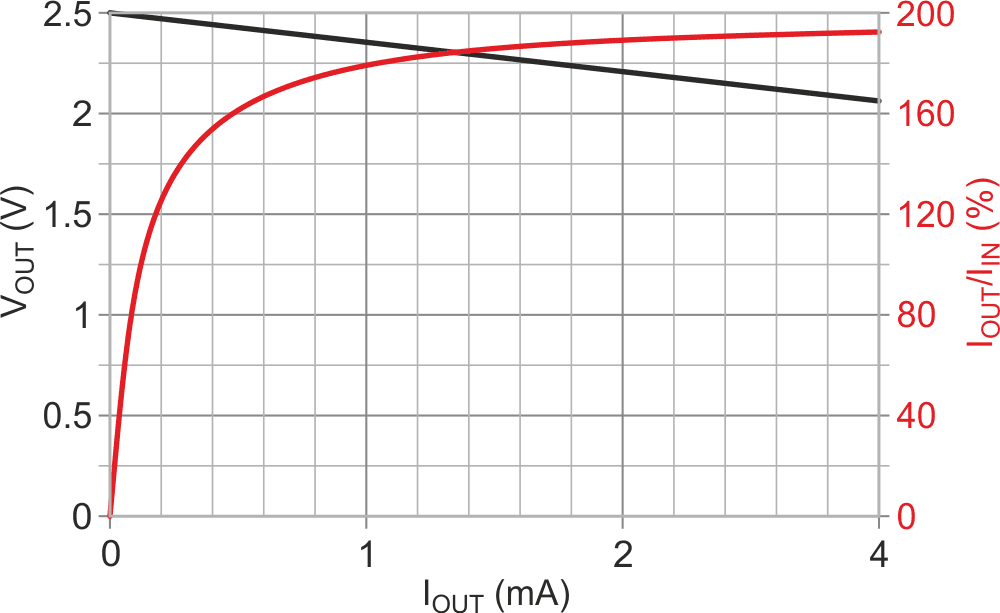
The combined effect on VOUT versus IOUT amounts to an effective impedance of 150 Ω for VIN = 5 V and is plotted in Figure 2, along with current multiplication “efficiency”. Note that the latter soars past unity due to the fact that only half of the dollops of C2 charge (the Q+) are drawn from the VIN rail, while the Q– are supplied from residual voltage on C2, causing zero additional drain from the rail.
 |
|
| Figure 2. | Current multiplying charge-pump VOUT and IOUT/IIN current “efficiency” for VIN = 5 V. |
So, what is it good for?
Figure 3 suggests one useful application, generating nominally symmetrical ±VIN/2 bipolar rails from a single positive source with minimal current draw from the source.
 |
|
| Figure 3. | Current doubling charge pump plus voltage inverter makes an efficient bipolar rail splitter. |