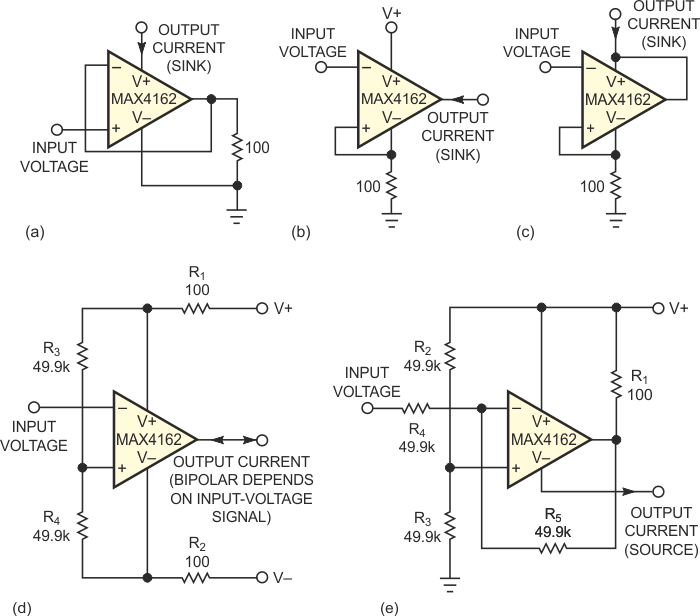
When you design for electronics applications, such as sensor or amplifier bias supplies or special waveform generators, a controlled constant-current source or sink circuit can serve as a useful building block. These circuits exhibit high dynamic-output impedance and deliver relatively large currents within an allowed range of compliance voltage. You can implement a constant-current circuit with an op amp and a discrete external transistor, but you can also design a bipolar version of a current source or sink around a single op amp and a few resistors (Figure 1). The constant-current sink circuits in Figure 1a through Figure 1c offer various compromises between precision, dynamic impedance, and compliance range.
 |
||
| Figure 1. | This compendium of constant-current circuits includes current sinks (a, b, and c), a bipolar sink or source (d), and a current source (e). |
|
The circuit in Figure 1d describes a bipolar current source with a simpler feedback configuration than that of the usual Howland-current pump, which requires positive feedback and presents variable input impedance. Figure 1e shows a constant-current source. All of these circuits exhibit excellent linearity of output current with respect to input voltage.
 |
||
| Figure 2. | These graphs show output current versus output-voltage characteristics for the circuits in Figure 1. Note that for b and c, the dynamic-output-impedance characteristic closely resembles that of an ideal current source: ΔVOUT/ΔVIN = ∞. |
|
The output from the circuit in Figure 1a includes an uncertainty due to the op amp's quiescent current, which adds to the calculated output current. For example, in most applications, you can neglect the MAX4162 op amp's quiescent current of approximately 25 µA. The circuit in Figure 1b behaves similarly, but its quiescent current subtracts from the ideal output-current value. The circuit in Figure 1c provides a current sink with no quiescent-current error, and the circuit in Figure 1d presents a bipolar output – that is, it sinks or sources current – depending on the polarity of the input voltage. Its performance depends on close matching for the resistor pairs R1 and R2 and R3 and R4 and good tracking of the positive- and negative-power-supply voltages. Any difference between the absolute values of the supply voltages appears as an offset current at 0 V input voltage. To achieve insensitivity to power-supply-voltage variations, the current-source circuit in Figure 1e requires close matching of resistor pairs R2 and R3 and R4 and R5.
You can use the following equations to calculate output currents for the circuits in Figure 1. Note that RLOAD = 100 Ω in these examples. In Figure 1a,
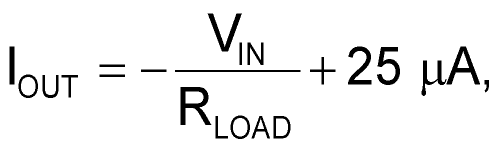
in Figure 1b,
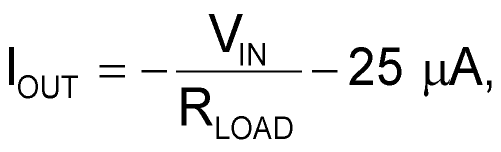
in Figure 1c,
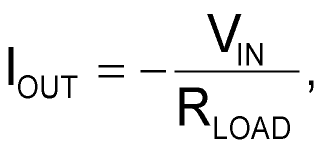
in Figure 1d,
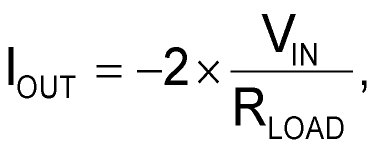
and, in Figure 1e,
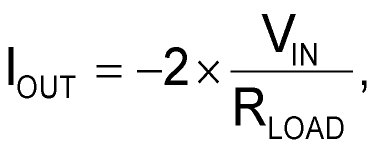
The equation for circuit Figure 1d assumes perfect matches – that is, R3 = R4, R1 = R2, and V+ = V–. It also assumes that R4 is much greater than R1.
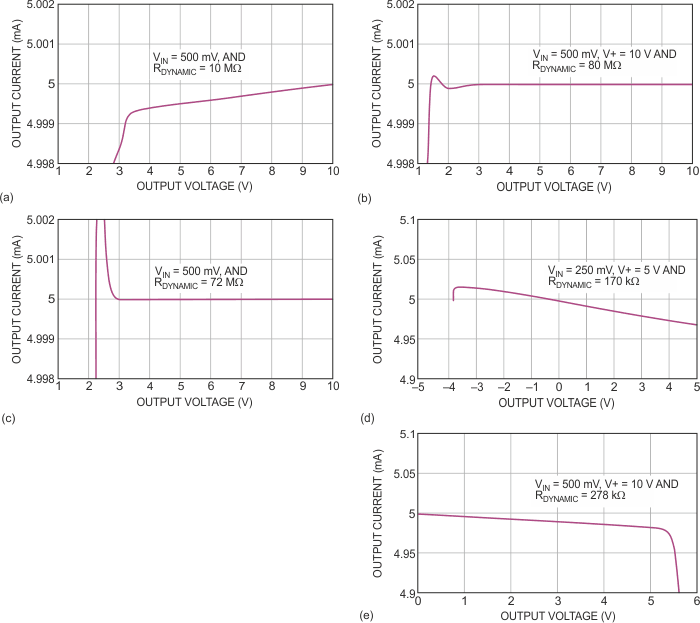
For a fixed value of output current in each of the five circuits in Figure 1, the graphs of Figure 2 show the circuits' dynamic impedance, RDYNAMIC, and range of useful output voltage (current compliance). The graphs show a high nominal output current of 5 mA to better display the higher end of the current-amplitude range. Depending on your application, you can optimize each circuit's dynamic impedance and current range through a judicious choice of op amps and resistor values.
